АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вопрос 2 Формула апостериорной вероятности Байеса

Читайте также:
  1. II. Вопросительное предложение
  2. VII. Вопросник для анализа учителем особенностей индивидуального стиля своей педагогической деятельности (А.К. Маркова)
  3. X. примерный перечень вопросов к итоговой аттестации
  4. Аграрный вопрос
  5. Анализ вероятности
  6. Барометрическая формула
  7. Барометрическая формула. Распределение Больцмана.
  8. Болгарский вопрос. Соборы на Западе на Востоке. Окончательное разделение 1054 года
  9. Более подробно вопрос об объектах экологических общественных отношений рассмотрен в главе II учебника. 1 страница
  10. Более подробно вопрос об объектах экологических общественных отношений рассмотрен в главе II учебника. 1 страница
  11. Более подробно вопрос об объектах экологических общественных отношений рассмотрен в главе II учебника. 1 страница
  12. Более подробно вопрос об объектах экологических общественных отношений рассмотрен в главе II учебника. 10 страница

Формула Байеса

Пусть H1,H2,...,Hn - полная группа событий и А Ì  – некоторое событие. Тогда по формуле для условной вероятности Здесь P(Hk /A) – условная вероятность события (гипотезы) Hk или вероятность того, что Hk реализуется при условии, что событие А произошло. По теореме умножения вероятностей числитель формулы (*) можно представить в виде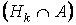

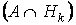
P = P= P(A /Hk) P(Hk) Для представления знаменателя формулы (*) можно использовать формулу полной вероятности

P(A) Теперь можно получить формулу, называемую формулой Байеса:

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |

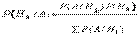
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)