 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Момент силы
 Пусть частица движется под действием силы
Пусть частица движется под действием силы  и ее положение в пространстве в некоторый момент времени
и ее положение в пространстве в некоторый момент времени 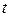 определяет радиус-вектор
определяет радиус-вектор  , проведенный из точки 0, являющейся началом координат (рис. 6.1).
, проведенный из точки 0, являющейся началом координат (рис. 6.1).
Назовем моментом силы  относительно точки 0 вектор
относительно точки 0 вектор  , равный векторному произведению векторов
, равный векторному произведению векторов  и
и  :
:
 (6.1)
(6.1)
Рис. 6.1
Направления векторов  и
и  связаны правилом правого винта (если направить указательный палец правой руки по вектору
связаны правилом правого винта (если направить указательный палец правой руки по вектору  , а средний — по вектору
, а средний — по вектору  , то отогнутый большой палец покажет направление вектора
, то отогнутый большой палец покажет направление вектора  (рис. 6.1)). Модуль момента силы
(рис. 6.1)). Модуль момента силы
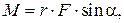 (6.2)
(6.2)
где 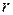 и
и  — модули векторов
— модули векторов  и
и  ; α — угол между векторами
; α — угол между векторами  и
и 
Назовем прямую, вдоль которой направлена сила, линией действия силы, а расстояние  от линии действия силы до точки 0 — плечом силы относительно точки 0. Как видно из рис. 6.1,
от линии действия силы до точки 0 — плечом силы относительно точки 0. Как видно из рис. 6.1,

откуда
 (6.3)
(6.3)
Проекция  вектора
вектора  на координатные оси
на координатные оси  называют моментами силы относительно этих осей. Например,
называют моментами силы относительно этих осей. Например,  — момент силы относительно оси
— момент силы относительно оси 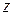 .
.
Теперь перейдем к рассмотрению вращения твердого тела вокруг неподвижной оси 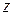 . Причиной этого вращения может быть сила
. Причиной этого вращения может быть сила  , приложенная к какой-либо частице тела, отстоящей от оси
, приложенная к какой-либо частице тела, отстоящей от оси 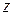 на некотором расстоянии
на некотором расстоянии 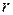 . Под действием силы
. Под действием силы  эта частица, а также все остальные частицы твердого тела будут двигаться по различным окружностям, центры которых лежат на оси
эта частица, а также все остальные частицы твердого тела будут двигаться по различным окружностям, центры которых лежат на оси 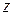 , а твердое тело вращаться с ускорением
, а твердое тело вращаться с ускорением  вокруг оси
вокруг оси 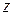 .
.
Расчет показывает, что для данного твердого тела и определенной оси вращения 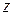 проекция
проекция  углового ускорения пропорциональна проекции
углового ускорения пропорциональна проекции  момента силы
момента силы  :
:
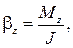 (6.4)
(6.4)
где 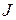 — положительная скалярная величина, называемая моментом инерции твердого тела относительно оси
— положительная скалярная величина, называемая моментом инерции твердого тела относительно оси 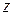 .
.
По определению
 (6.5)
(6.5)
где 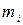 и
и 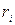 — масса и расстояние
— масса и расстояние 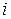 -й частицы тела от z;
-й частицы тела от z;
N — число частиц, из которых состоит тело.
Для нахождения момента инерции твердого тела от выражения (6.5) переходят к формуле

(6.6)
где  — масса элемента тела, находящего на расстоянии
— масса элемента тела, находящего на расстоянии 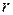 от оси
от оси 
В Приложении приведены моменты инерции 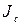 некоторых однородных твердых тел относительно оси
некоторых однородных твердых тел относительно оси  , проходящей через центр масс тела. Зная момент инерции
, проходящей через центр масс тела. Зная момент инерции 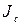 , можно определить момент инерции
, можно определить момент инерции 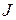 относительно любой оси, параллельной оси
относительно любой оси, параллельной оси  и отстоящей от нее на расстоянии
и отстоящей от нее на расстоянии  (теорема Штейнера):
(теорема Штейнера):
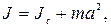
(6.7)
где  — масса тела.
— масса тела.
Соотношение (6.4), записанное в виде
 (6.8)
(6.8)
называют основным уравнением динамики вращения твердого тела.
Если на тело действует не одна, а несколько сил, то в уравнении (6.8) Mz — суммарный момент сил относительно оси 
При повороте тела на элементарный угол d φсила  совершает элементарную работу
совершает элементарную работу
 (6.9)
(6.9)
Работа силы  при повороте тела на угол
при повороте тела на угол 
 (6.10)
(6.10)

Мощность этой силы
 (6.11)
(6.11)
где 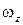 — проекция угловой скорости тела на ось вращения
— проекция угловой скорости тела на ось вращения 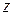 .
.
Пример 6.1. Колесо диаметром D = 60 см вращается под действием касательной к ее ободу силы F = 10 H. Найти момент инерции 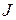 колеса относительно неподвижной оси
колеса относительно неподвижной оси 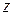 , проходящей через центр колеса перпендикулярно его плоскости, если за промежуток времени от
, проходящей через центр колеса перпендикулярно его плоскости, если за промежуток времени от 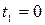 до t 2 = 3 c проекция
до t 2 = 3 c проекция 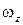 угловой скорости колеса изменилась от 0 до 9 рад/с.
угловой скорости колеса изменилась от 0 до 9 рад/с.
Дано:
D = 60 см
F = 10 H
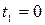 t 2 = 3 c
t 2 = 3 c
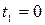
 

| Решение

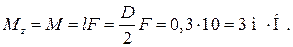

 
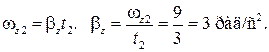
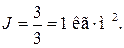
|
  J –? J –?
|
Ответ: 
Пример 6.2. Закон вращения шара,  где А = 2 рад,
где А = 2 рад,  Шар вращается вокруг оси
Шар вращается вокруг оси 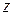 , проходящей через его центр. Найти среднюю мощность
, проходящей через его центр. Найти среднюю мощность 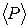 , развиваемую силой, действующей на шар при его вращении от
, развиваемую силой, действующей на шар при его вращении от 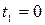 до момента времени
до момента времени 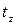 его остановки. Радиус шара
его остановки. Радиус шара  Масса шара
Масса шара 
Дано:



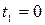

| Решение




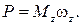
|

|


(см. Приложение А)

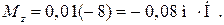



Ответ: 

Поиск по сайту: