Энергия электрического поля

Имеем заряженный проводник. Увеличим его заряд на dq. Для этого надо совершить работу против сил электрического поля (одноименные заряды отталкиваются). Работа, совершаемая внешними силами при переносе заряда dq из бесконечности на проводник,

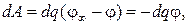(42.1)

где φ — потенциал проводника (мы приняли потенциал на бесконечности ).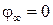

Для увеличения заряда проводника на q надо совершить работу

(42.2)

где C — электроемкость проводника (см. формулу (40.4)). Знак минус указывает, что работа совершается против сил электрического поля. При разряде проводника работа совершается уже силами электрического поля, поэтому эту работу записывают со знаком плюс. Так как совершенная при разряде проводника работа равна сообщенной проводнику энергии, то

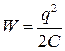(42.3)

есть электрическая энергия заряженного проводника.

Получим выражение для электрической энергии плоского конденсатора. С учетом выражений (41.7) и (41.9) перепишем формулу (42.3) в виде

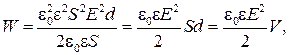(42.4)

где 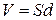— объем между обкладками конденсатора.

Так как электрическое поле, создаваемое конденсатором, практически полностью сосредоточено между его обкладками, то выражение (42.4) определяет энергию электрического поля в объеме V. Разделив W на V, получим объемную плотность энергии электрического поля:

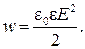(42.5)

Формула (42.5) справедлива не только для поля плоского конденсатора, но и для любого электрического поля. Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенную в любом объеме V:

(42.6)

Поиск по сайту: