Намагничивание магнетика

В настоящее время установлено, что молекулы многих веществ обладают собственным магнитным моментом 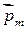, обусловленным внутренним круговым движением зарядов (молекулярным током).

Такую молекулу можно представить в виде элементарного контура с током. Магнитные моменты молекул ориентированы хаотически из-за теплового движения молекул. Есть вещества, молекулы которых не обладают собственным магнитным моментом.

Под действием внешнего магнитного поля с магнитной индукцией 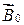те и другие вещества намагничиваются, и поэтому в этом случае их называют магнетиками. Собственные магнитные моменты молекул магнетика устанавливаются по полю ().

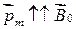В молекулах, не обладающих собственным магнитным моментом, индуцируются элементарные круговые токи, 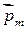которых тоже устанавливаются по полю.

Для количественного описания намагничивания магнетика берут магнитный момент единицы объема магнетика

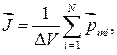(54.1)

где 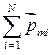— сумма магнитных моментов N молекул, заключенных в элементарном (очень малом) объеме 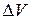магнетика. Вектор называют намагниченностью магнетика.

На рис. 54.1 изображен схематически намагниченный однородный магнетик. Из рисунка видно, что намагничивание сопровождается возникновением тока , текущего по боковой поверхности магнетика (молекулярные токи в местах соприкосновения компенсируются, так как текут в противоположных направлениях).

Этот ток называют током намагничивания, в отличие от обычного тока, текущего по проводнику и поэтому называемого током проводимости.

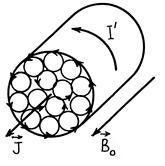
Рис. 54.1

В результате появления тока намагничивания в магнетике возникает магнитное поле, создаваемое этим током. Магнитная индукция поля в магнетике равна сумме магнитных индукций 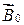поля, создаваемого током проводимости (внешнего поля), и поля, создаваемого током намагничивания:

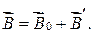(54.2)

§ 55. Вектор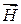

Теорема о циркуляции вектора в магнетике имеет вид

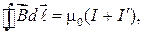(55.1)

где I и — токи проводимости и намагничивания, охватываемые контуром. Расчет вектора в магнетике с использованием соотношения (55.1) затруднителен, так как заранее не известен ток намагничивания в магнитном поле. Это затруднение можно обойти, воспользовавшись теоремой о циркуляции вектора :

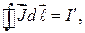(55.2)

циркуляция вектора по произвольному контуру равна , где — алгебраическая сумма токов намагничивания, охватываемых этим контуром. Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта (если вращать винт в направлении обхода по контуру, то направление движения винта должно показывать направление тока). В противном случае ток считается отрицательным.

Подставляя

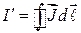
в соотношение (55.1), получаем

откуда

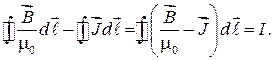(55.3)

Введем вектор

(55.4)

и запишем выражение потока вектора 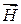в виде

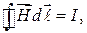(55.5)

которое представляет теорему о циркуляции вектора 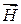: циркуляция вектора 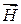по произвольному контуру равна I, где I — алгебраическая сумма токов проводимости, охватываемых этим контуром. Правило знаков для токов то же, что и в случае циркуляции вектора (см. § 50).

Для многих магнетиков

(55.6)

где χ — безразмерная величина, называемая магнитной восприимчивостью вещества. Эта величина не зависит от 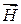и является характеристикой магнетика. Она может быть как положительной, так и отрицательной. Магнетики с 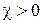называют парамагнетиками, с 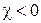— диамагнетиками. У парамагнетиков векторы и 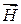имеют одинаковое направление, у диамагнетиков — противоположное.

Подставляя выражение (55.6) в соотношение (55.4), получаем

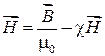
или

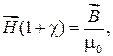
откуда

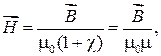(55.7)

где 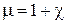— безразмерная положительная величина, называемая магнитной проницаемостью вещества. Эта величина, как и χ, является характеристикой магнетика. Для вакуума 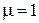. У парамагнетиков 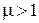, у диамагнетиков 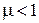. Так как у пара- и диамагнетиков χ очень мало (порядка 10^–6–10^–3), их магнитные проницаемости мало отличаются от единицы.

Из соотношения (55.7) имеем

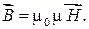(55.8)

Следовательно, используя теорему о циркуляции вектора 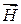, можно определить вектор 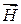в любой точке магнитного поля в магнетике, а затем из соотношения (55.8) найти магнитную индукцию поля в этой точке.

Пример 55.1. Соленоид, по которому течет ток силой I, заполнен магнетиком с магнитной проницаемостью μ. Число витков на единице длины соленоида равно n. Найти магнитную индукцию B поля в соленоиде.

Дано:   I   μ   n	Решение   Изобразим продольный разрез соленоида (рис. 55.1). Возьмем произвольную точку внутри соленоида и проведем через эту точку контур прямоугольника, как показано на рис. 55.1. Определим циркуляцию вектора 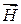по контуру, обходя его по часовой стрелке. Можем написать
В –?
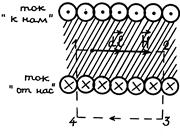Рис. 55.1	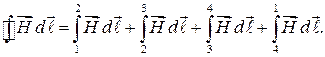(55.9)   В соотношении (55.9)

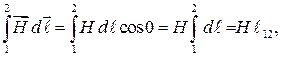
где ℓ₁₂ — длина стороны 12 прямоугольника (мы учли, что H = const, так как сторона 12 является одной из линий вектора ),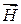

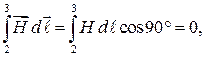
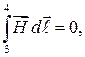
так как вне соленоида ,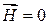

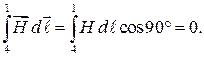
Таким образом,

(55.10)

Согласно теореме о циркуляции вектора 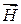(55.5)

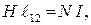(55.11)

где N — число витков на длине ℓ₁₂ соленоида, откуда

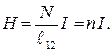(55.12)

Воспользовавшись соотношением (5.8), находим магнитную индукцию B:

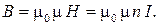(55.13)

Поиск по сайту: