Интерференция света

Пусть две плоские световые волны с одинаковой частотой ω и одинаковым направлением колебаний вектора встречаются в некоторой точке P пространства. Расчет показывает, что модуль амплитуды колебаний вектора результирующей волны

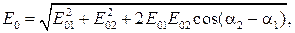(64.1)

где E ₀₁, E ₀₂ и 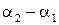— модули амплитуд и разность фаз складываемых волн в точке P.

С учетом выражения (63.5) результирующая интенсивность света в точке P

(64.2)

Если разность фаз 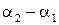остается постоянной во времени, то световые волны называют когерентными. В тех точках, для которых 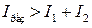. В тех точках, для которых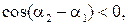 . Таким образом, при наложении когерентных световых волн в пространстве образуется постоянное во времени распределение интенсивности света. Это явление называют интерференцией света.

Рассмотрим интерференцию двух когерентных световых волн с одинаковой интенсивностью I. Тогда из соотношения (64.2) следует

(64.3)

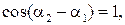
В тех точках, для которых — максимальная интенсивность света. В тех точках, для которых — минимальная (нулевая) интенсивность света.

Когерентные световые волны можно получить, разделив волну, излучаемую одним источником, на две части. Если заставить эти две волны пройти разные оптические пути и встретиться в некоторой точке P, то в точке P будем наблюдать интерференцию (рис. 64.1).

Пусть разделение на две когерентные волны происходи в точке O.

Рис. 64.1

S ₁ — путь, проходимый от O до P первой волной в первой среде с показателем преломления n ₁; S ₂ — путь, проходимый от O до P второй волной во второй среде с показателем преломления n ₂. Если в точке O фаза колебаний обеих волн равна ω t, то в точке P первая волна возбудит колебания с фазой а вторая волна — с фазой где v ₁ и v ₂ — скорости распространения первой и второй волн. Разность фаз колебаний в точке P

(64.4)

(мы учли формулы (63.1) и (63.3)).

Назовем произведение S n оптическим путем, проходимым световой волной, а

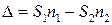(64.5)

— оптической разностью хода двух световых волн от O до P.

С учетом выражения (64.5) перепишем соотношение (64.4) в виде

(64.6)

Если 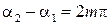, где то в точке P будет максимальная интенсивность света: . Из соотношения (64.6) следует

или

(64.7)

— условие интерференционного максимума.

Если 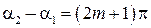, где то в точке P будет минимальная (нулевая) интенсивность света: . Из соотношения (64.6) следует

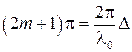
или

(64.8)

— условие интерференционного минимума.

Поиск по сайту: