Вопрос 25 Дисперсия света. Методы наблюдения. Электронная теория дисперсии света. Спектры

Дисперсией света называется зависимость показателя преломления nвещества от частоты ν(длины волн λ) света или зависимость фазовой скорости световых волн от их частоты.

Спектр, показанный на рис. является призматическим. Фиолетовые волны преломляются сильнее красных, т.к. длина волны красных волн больше, чем у фиолетовых, а частота, соответственно, меньше, то показатель преломления красных волн будет меньше, чем у фиолетовых.

Призмы часто используются в различных спектроскопах (Спектроскоп (спектрометр, спектрограф) (от спектр и др. - греч. σκοπ?ω — смотрю) — оптический прибор для визуального наблюдения спектра излучения.) Отличие спектрометра от спектрографа заключается в том, что в спектрометре происходит визуальное наблюдение спектра с помощью глаз, а в спектрографе используется какой-либо способ записи спектра – фотопластинка, самописец, фотоумножитель или фотоэлемент, цифровая фотокамера и т.п. Те и другие используются для быстрого качественного спектрального анализа веществ в химии, металлургии (например, стилоскоп) и т. д).

Дисперсия света называется нормальной, если показатель преломления монотонно убывает с увеличением длины волны (возрастает с увеличением частоты).

Макроскопическая теория Максвелла не может объяснить дисперсию света. Из теории Максвелла следует, что 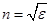, при μ = 1.

Для воды ε = 81, следовательно, , а в действительности n в =1,33. Такое противоречие между теорией Максвелла и экспериментом возникает вследствие того, что мы правильно применяем формулу ε0 = 81, которая справедлива только в статическом поле (ω = 0). Молекулы воды постоянно ориентируются в переменном электрическом поле. Электрическое поле световой волны изменяется по гармоническому закону.

ε(ω) < ε(0), поэтому n(ω) < n(0). Т.е. для каждой частоты будет свой показатель преломления. Поэтому нужно учитывать зависимость n от частоты.

Явление дисперсии можно объяснить, рассматривая взаимодействие световой волны с веществом. Такое стало возможным благодаря классической электронной теории Лоренца.

Согласно классической электронной теории электроны в атоме совершают колебания под действием квазиупругой силы. Световая волн, падающая на диэлектрик, заставляет электроны, находящиеся в атоме этого диэлектрика, совершать вынужденные колебания, частота которых совпадает с частотой вынуждающей силы. Но электроны, движущиеся ускоренно излучают электромагнитные волны. Эти вторичны волны, излучаемые электронами атомов вещества, имеют ту же частоту, что и падающая волна. Начальные фазы могут различаться. Эти вторичные волны интерферируют с падающей волной, и в веществе распространяется результирующая волна, направление которой совпадает с направлением падающей волны, скорость которой зависит от частоты (а в вакууме равна скорости света). Следовательно, показатель преломления n зависит от частоты ω.

где χ – диэлектрическая восприимчивость вещества, Р – вектор поляризации (результирующий дипольный момент единицы объёма).

Согласно теории Максвелла

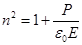при μ = 1.

В условиях, когда на вещество падает световая волна, электрическое поле изменяется столь быстро, что поляризуемость (нас будет интересовать только электронная, т.е. индуцированная полем световой волны) не успевает изменяться за полем. В этом случае

где n0 – количество атомов в единице объёма, РЕ – индуцированный дипольный момент одного атома. Можно показать, что наиболее сильному воздействию электрического поля световой волны подвергаются наиболее слабо связанные с ядром электроны, так называемые оптические электроны. Для простоты считаем, что каждый атом содержит один оптический электрон. Тогда х - смещение. т.е. n зависит от смещения электронов в атоме, под действием поля световой волны. На электрон, находящийся в атоме действует также силы:

квазиупругая – из-за наличия связи электрона с ядром: сила сопротивления Вынуждающая сила со стороны световой волны

Под действием этих сил электрон начинает совершать вынужденные колебания

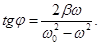
Для простоты рассмотрения будем пренебрегать затуханием колебаний. В этом случае

Из последней формулы видно, что n зависит от частоты падающего света, так же как и ε. Если ω0 > ω, то n существует, если ω0 = ω, то n терпит разрыв 2-го рода. В том случае, если атом содержит несколько валентных электронов: Если учесть затухание (β ≠ 0), то мы получаем формулу, которая даёт хорошее соответствие с экспериментальной кривой)

Поиск по сайту: