Уравнение Шредингера. является решением дифференциального уравнения

Волновая функция

является решением дифференциального уравнения. Получим его. Пусть микрочастица движется в потенциальном поле и ее волновая функция не зависит от времени. Можем написать

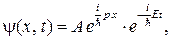
откуда не зависит от времени. Продифференцируем ψ дважды по x.

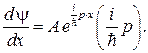
откуда

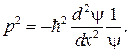
Свяжем E и p:

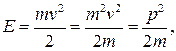
откуда

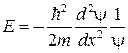
или

(82.1)

Механическая энергия микрочастицы

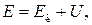
где — кинетическая энергия микрочастицы; U — потенциальная энергия микрочастицы. В уравнении (82.1) E = . В случае потенциального поля 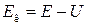. Тогда имеем

(82.2)

Уравнение (82.2) называют стационарным уравнением Шредингера для микрочастицы, движущейся в потенциальном поле вдоль оси x.

Уравнение Шредингера является основным уравнением квантовой механики. Оно не выводится из других уравнений, а является исходным основным предположением (постулатом), справедливость которого доказывается тем, что все вытекающие из него следствия самым точным образом согласуются с опытом.

Поиск по сайту: