КОНТРОЛЬНЫЕ ЗАДАНИЯ 1

Вариант 1

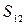1. Скорость частицы a = 1 м/с². Найти путь частицы за время от t ₁ = 2 c до t ₂ = 3 c.

2. Обруч и диск, имеющие одинаковую массу , катятся без скольжения по горизонтальной поверхности с одной и той же скоростью v. Кинетическая энергия обруча E_к = 39,24 Дж. Найти кинетическую энергию диска.

3. Лодка массой m = 200 кг с находящимся в ней человеком массой m = = 50 кг стоит в спокойной воде. Человек начинает идти вдоль лодки со скоростью относительно лодки. С какой скоростью v _л движется при этом лодка по отношению к воде? Сопротивление воды движению лодки не учитывать.

Вариант 2

1. Закон вращения тела , рад, где А = 10 рад; B = = 10 рад/c; С = 2 рад/c². Найти модуль ускорения частицы тела, находящегося на расстоянии r = 0,1 м от оси вращения, в момент времени t ₁ = 4 c.

2. Под действием силы F = 10 Н частица движется вдоль оси по закону где C = 1 м/с². Найти массу частицы.

3. Частица совершает гармоническое колебания вдоль оси Амплитуда колебаний частицы А = 5 см. Период колебаний частицы T = 4 c. Найти модуль v _max максимальной скорости частицы.

Вариант 3

1. Закон движения частицы где и — положительные постоянные. Найти скорость частицы.

2. Шар катится без скольжения по горизонтальной поверхности. Кинетическая энергия шара E_к = 14 Дж. Определить кинетические энергии и поступательного и вращательного движения шара.

3. Шайбу пустили снизу вверх на горку со скоростью шайбы v ₁ = 10 м/с. Определить высоту 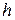, на которой скорость шайбы v ₂ = 7 м/с. Трением пренебречь.

Вариант 4

1. Закон движения частицы м, где b = 1 м/с; с = 1 м/с³. Найти ускорение 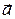частицы в момент времени t ₁ = 3 c.

2. Скорость пути в момент времени 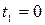равна v ₁ = 800 м/с. При движении в воздухе в момент времени t ₂ = 0,8 c скорость пули уменьшилась до v ₂ = = 200 м/с. Модуль силы сопротивления воздуха пропорционален квадрату скорости: Масса пули m = 10 г. Определить коэффициент сопротивления .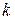

3. Человек массой m _ч = 60 кг стоит на краю горизонтального диска массой m _д = 240 кг. Человек совершает равномерное перемещение по краю диска на угол относительно диска и останавливается. Считая человека частицей, найти угол поворота φ_д диска вокруг оси, проходящей через центр диска перпендикулярно его плоскости.

Вариант 5

1. Закон вращения тела рад. Найти модуль β углового ускорения тела в момент времени его остановки.

2. Частица массой движется под действием силы , где — постоянный вектор; ω — положительная константа. В момент 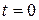радиус-вектор и скорость частицы равны нулю. Найти закон движения частицы .

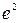3. Амплитуда колебаний частицы за время уменьшилась в раз. Найти коэффициент затухания β.

Вариант 6

1. Колесо вращается вокруг своей оси по закону рад, где B = 1 рад/c; С = 1 рад/c²; и D = 1 рад/c³. Найти радиус обода колеса, если известно, что в момент времени t ₁ = 2 c частицы обода колеса имеют нормальное ускорение м/c².

2. Сила , Н, приложена к частице с радиусом-вектором м. Найти момент силы относительно начала координат.

3. Закон движения частицы см. Найти модуль v _max максимальной скорости частицы.

Вариант 7

1. Закон вращения тела , рад, где a = 5 рад/c². Найти средний модуль 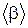углового ускорения тела за промежуток времени от 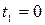до t ₂ = = 2 c.

2. Тело массой m = 1 кг брошено вертикально вверх со скоростью v ₁ = 10 м/с. Максимальная высота подъема тела м. Найти по этим данным работу силы сопротивления воздуха за время подъема тела.

3. Частица, положение которой относительно начала отсчета декартовой системы координат (точка О) дается радиусом-вектором имеет импульс кг ∙ м/с. Определить момент импульса 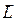относительно точки О.

Вариант 8

1. Закон движения частицы 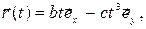м, где b = 1 м/с; с = 2 м/с³. Найти модуль ускорения частицы в момент времени t = 3 c.

2. Частица массой движется вдоль оси под действием силы где 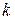— постоянная. В момент времени 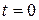координата и скорость Найти закон движения частицы .

3. На краю горизонтального диска массой 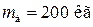и радиусом R = 2 м стоит человек массой m _ч = 80 кг. Считая человека частицей, найти угловую скорость ω_д вращения диска вокруг вертикальной оси, проходящей через центр диска, если человек идет вдоль края диска со скоростью относительно диска.

Вариант 9

1. Закон вращения тела рад, где a = 6 рад/с²; b = 2 рад/с³. Найти средний модуль угловой скорости тела за промежуток времени от 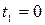до момента остановки тела.

2. Частица массой начинает двигаться со скоростью под действием силы где — положительная постоянная. Найти зависимость скорости частицы от времени.

3. Логарифмический декремент затухания . Во сколько раз уменьшится амплитуда колебаний частицы за одно колебание?

Вариант 10

1. Закон движения частицы , где и — положительные постоянные. Найти модуль v (t) скорости частицы.

2. Закон вращения тела рад, где A = 2 рад; B = = 16 рад/c; C = – 2 рад/c². Момент инерции тела относительно оси вращения 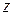J = 50 кг ∙ м². Найти мощность 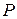силы в момент времени t ₁ = 3 c.

3. Закон движения частицы t, м. Найти модуль 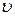скорости частицы в момент времени .

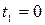Вариант 11

1. Закон вращения тела 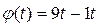³, рад. Найти средний модуль 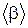углового ускорения тела за промежуток времени от 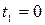до момента остановки тела.

2. Закон движения частицы где и ω — положительные постоянные. Считая известной массу частицы в кг, найти силу , действующую на частицу.

3. На полу стоит тележка в виде длиной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса человека m _ч = 60 кг, масса тележки m _т = 20 кг. С какой скоростью v _т относительно пола будет двигаться тележка, если человек будет двигаться вдоль доски со скоростью относительно доски? Массой колес и трением пренебречь.

Вариант 12

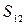1. Закон движения частицы м. Вычислить путь , пройденный частицей за первые 10 с движения.

2. Стержень вращается вокруг оси , проходящей через его середину, согласно уравнению рад, где A = 2 рад/с; B = 0,2 рад/c³. Определить вращающий момент , действующий на стержень в момент времени
t ₁ = 2 c после начала движения, если момент инерции стержня J = 0,048 кг ∙ м².

3. Частица совершает гармонические колебания вдоль оси . Амплитуда колебаний частицы А = 5 см. Период колебаний частицы T = 4 с. Найти модуль максимального ускорения частицы.

Вариант 13

1. Закон вращения тела где a = 6 рад/с². Найти момент времени , в который тело останавливается.

2. К краю диска массой m = 50 кг и радиусом R = 0,5 м приложена касательная сила F = 98,1 Н. В момент времени 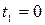частота вращения диска , в момент времени частота вращения 100 об/с. Определить момент времени .

3. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса человека m _ч = 60 кг, масса тележки m _т = 20 кг. Найти, на какое расстояние переместится человек относительно пола при его переходе на другой конец доски. Длина доски l = 2 м. Массой колес и трением пренебречь.

Вариант 14

1. Закон движения частицы м, где a = 1 м/с; b = 2 м/с². Найти среднее ускорение частицы за промежуток времени от t ₁ = 2 c до
t ₂ = 4 c.

2. Обруч и сплошной цилиндр, имеющие одинаковую массу m = 2 кг, катятся без скольжения по горизонтальной поверхности с одинаковой скоростью Найти кинетические энергии и этих тел.

3. Закон движения частицы м. Найти модуль v скорости частицы в момент времени , где — период колебания частицы.

Вариант 15

1. Закон движения частицы 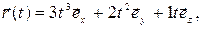м. Найти модуль ускорения частицы в момент t ₁ = 4 c.

2. Находясь под действием постоянной силы , Н, частица переместилась из точки 1 с радиусом-вектором , м. Какая при этом совершена работа?

3. Столб высотой h = 3 м падает из вертикального положения на землю. Вычислить скорость v верхнего конца столба в момент его удара о поверхность земли. Поверхность земли горизонтальна.

Вариант 16

1. Закон движения частицы м, где b = 1 м/с; c = 2 м/с³. Найти проекцию ускорения частицы в момент времени t ₁ = 3 с.

2. Закон вращения тела , рад, где A = 2 рад; B = = 16 рад/c; C = – 2 рад/c². Момент инерции тела относительно оси вращения 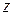J = 50 кг ∙ м². Найти среднюю мощность 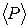силы за промежуток времени от
t ₁ = 2 с до t ₂ = 4 с.

3. Лодка массой m _л = 300 кг с находящимся в ней человеком массой m _ч = 70 кг стоит в спокойной воде. Человек начинает идти вдоль лодки и проходит расстояние l = 1 м. Найти смещение лодки относительно воды при этом переходе человека. Сопротивление воды движению лодки не учитывать

Вариант 17

1. Частица движется со скоростью где b = = 1 м/с². Найти модуль ускорения частицы.

2. Однородный стержень длиной l = 1 м и массой m = 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси , проходящей через середину стержня. С каким модулем β углового ускорения вращается стержень, если на него действует момент силы 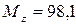м ∙ мН?

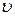3. Закон движения частицы t, м. Найти модуль скорости частицы в момент времени , где — период колебания частицы.

Вариант 18

1. Закон движения частицы , м. Найти модуль v скорости частицы в момент времени t ₁ = 1 с.

2. Скорость частицы массой m = 5 кг изменяется со временем 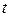по закону 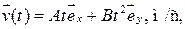где A = 1 м/с²; B = 2 м/с³. Найти силу , действующую на частицу в момент времени t ₁ = 1 с.

3. Карандаш, длиной l = 15 cм, поставленный вертикально, падает на стол. Какую угловую скорость ω и линейную скорость 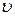будет иметь в конце падения верхний конец карандаша?

Вариант 19

1. Закон вращения тела Найти средний модуль угловой скорости тела за промежуток времени от 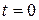до момента остановки тела.

2. Для частицы массой m = 10 кг известна зависимость ее скорости от времени где A = 1 м/с²; B = 2 м/с³; C = 3 м/с⁴. Найти мощность 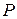силы, действующей на частицу в момент времени t ₁ = 2 с.

3. Закон движения частицы массой m = 50 кг имеет вид , где A = 10 см; Найти проекцию силы, действующей на частицу, когда фаза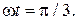

Вариант 20

1. Закон движения частицы м, где b = 1 м/с; c = 2 м/с³. Найти путь 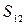частицы за время от t ₁ = 1 с до t ₂ = 5 с.

2. Однородный цилиндр радиусом R = 0,2 м и массой m = 5 кг вращается вокруг своей оси. Зависимость модуля угловой скорости вращения цилиндра от времени 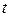дается уравнением рад/с, где B = 8 рад/c². Найти касательную силу , приложенную к боковой поверхности цилиндра, перпендикулярно его оси.

3. Частица, положение которой относительно начала отсчета декартовой системы координат (точки О) дается радиусом-вектором , м. имеем импульс , кг ∙ м/с. Определить проекции момента импульса 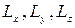относительно осей .

Вариант 21

1. Закон движения частицы м, где b = 1 м/с; c = 2 м/с². Найти проекцию ускорения частицы.

2. Сила , Н, приложена к частице с радиусом-вектором , м. Найти модуль 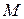момента силы относительно начала координат.

3. Человек массой m _ч = 60 кг стоит на краю горизонтального диска массой m _д = 300 кг. Человек совершает равномерное перемещение по краю диска и возвращается в исходную точку (на диск). Считая человека частицей, найти угол поворота диска вокруг оси, проходящей через центр диска перпендикулярно его плоскости.

Вариант 22

1. Диск радиусом R = 20 см вращается по закону рад, где A = 3 рад; B = – 1 рад/c; C = 0,1 рад/c³. Найти тангенциальное и нормальное ускорения частиц на краю диска в момент времени t ₁ = 10 с.

2. Находясь под действием постоянной силы 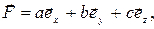Н, частица переместилась из точки 1 с радиусом-вектором м. в точку 2 с радиусом-вектором м. Какая при этом совершена работа?

3. За время амплитуда колебаний частицы уменьшается в 2 раза. За какое время амплитуда частицы уменьшится в 10 раз?

Вариант 23

1. Закон движения частицы м, где b = 1 м/с; c = 2 м/с². Найти проекцию v_x скорости частицы.

2. Шар массой m = 10 кг и радиусом R = 20 см вращается вокруг оси , проходящей через его центр. Закон вращения шара ³, рад, где B = 4 рад/c²; C = – 1 рад/c³. Определить момент силы в момент времени
t ₁ = 2 с.

3. Лодка массой m _л = 300 кг с находящимся в ней человеком массой m _ч = 80 кг стоит в спокойной воде. Человек начинает идти вдоль лодки со скоростью относительно лодки. С какой скоростью v _ч движется при этом человек относительно воды? Сопротивление воды движению лодки не учитывать.

Вариант 24

1. Закон вращения тела , рад, где a = 5 рад/с². Найти средний модуль угловой скорости тела за промежуток времени от 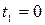до t ₂ = 2 с.

2. Шайбу массой m = 500 г пустили снизу вверх по горке со скоростью На высоте h = 3 м скорость шайбы Найти работу силы трения за время подъема шайбы.

3. Закон движения частицы см. Найти модуль максимального ускорения частицы.

Вариант 25

1. Модуль скорости частицы изменяется со временем 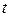по закону где и — положительные постоянные. Модуль ускорения частицы . Найти радиус кривизны траектории частицы в зависимости от времени .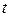

2. Однородный диск радиусом R = 20 см и массой m = 5 кг вращается вокруг оси 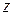, перпендикулярной его плоскости и проходящей через центр диска. Проекция угловой скорости диска где B = 4 рад/с². Найти касательную силу, действующую на обод диска.

3. Частица, положение которой относительно начала отсчета декартовой системы координат (точка О) дается радиусом-вектором м, имеет импульс кг ∙ м/с. Определить модуль 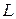момента импульса относительно точки .

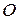Вариант 26

1. Закон вращения тела , рад, где B = 2 рад/c; C = = 1 рад/c³. Найти модуль ω угловой скорости через 2 c после начала движения.

2. Тело массой m = 0,1 кг бросили вертикально вверх со скоростью Упало тело в точку бросания со скоростью Найти работу силы сопротивления воздуха за время полета тела.

3. Закон движения частицы м. Найти модуль v скорости частицы в момент времени , где — период колебания частицы.

Вариант 27

1. Закон движения частицы м. Найти проекцию v_y скорости частицы в момент времени t ₁ = 5 с.

2. Частица массой движется под действием силы , где — постоянный вектор, — положительная константа. В момент 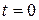скорость частицы = 0. Найти зависимость скорости частицы от времени .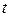

3. Частица совершает колебаний. За это время амплитуда колебаний частицы уменьшается в 2,7 раза. Чему равен логарифмический декремент затуханий λ?

Вариант 28

1. Закон вращения тела 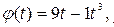рад. Найти модуль β углового ускорения в момент остановки тела.

2. Частица массой начинает двигаться со скоростью под действием силы где — положительная постоянная; — скорость частицы. Найти зависимость ускорения частицы от времени.

3. Закон движения частицы массой m = 16 г имеет вид x (t) = 4) см. Найти модуль максимальной силы, действующей на частицу.

Вариант 29

1. Частица движется со скоростью где a = = 1 м/с². Найти модуль v скорости частицы в момент времени t ₁ = 1 с.

2. Скорость частицы массой m = 5 кг изменяется со временем 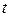по закону где A = 1 м/с²; B = 2 м/с³. Найти модуль силы, действующей на частицу в момент времени t ₁ = 1 с.

3. Лодка массой m _л = 300 кг с находящимся в ней человеком массой m _ч = 70 кг стоит в спокойной воде. Человек начинает идти вдоль лодки и проходит расстояние l = 1 м. Найти смещение человека относительно воды. Сопротивление воды движению лодки не учитывать.

Вариант 30

1. Закон движения частицы м, где b = 1 м/с; c = 2 м/с². Найти средний модуль ускорения частицы за промежуток времени от t ₁ = = 2 с до t ₂ = 4 с.

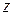2. Закон вращения однородного шара рад. Ось вращения совпадает с его диаметром D = 10 см. Масса шара m = 1 кг. Определить момент силы, действующей на шар.

3. Закон движения частицы массой имеет вид Найти модуль максимальной силы, действующей на частицу.

Поиск по сайту: