АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Соотношение неопределенностей Гейзенберга

Читайте также:
  1. А. Базовое системное соотношение.
  2. Б. Системное соотношение с измененным основным аргументом.
  3. Вопрос – 15 Понятие и признаки муниципальных образований. Виды мо в РФ. Соотношение административно-территориального и муниципально-территориального устройства РФ.
  4. Вопрос: Предмет и метод правового регулирования. Частное и публичное право. Материальные и процессуальные отрасли права. Соотношение национального и международного права.
  5. Вопрос: Соотношение понятий «форма» и «источник» права. Материальные, идеальные и юридические источники права.
  6. Вопрос: Способы изложения правовых норм в статьях нормативных актов. Соотношение нормы права и статьи нормативного акта.
  7. Глава VII СООТНОШЕНИЕ ЯЗЫКА С МЫШЛЕНИЕМ
  8. Закон эксцентрического расположения длинных проводников спиноталамического тракта и его топико-диагностическое значение: соотношение сегментов спинного мозга и тел позвонков
  9. И теоретический уровни, их соотношение
  10. Исполнительная власть и её соотношение с государственным управлением
  11. Как в экзистенциализме (особенно у Сартра) трактуется соотношение между существованием и сущностью человека?
  12. Каковы статус сравнительного правоведения и его соотношение со сравнительным методом?

 

Рис. 81.1
Естественно связать с движением микрочастицы, например, вдоль оси x, не непрерывную бесконечную волну, а цуг волн, имеющий ограниченную протяженность Δ x в пространстве (рис. 81.1). В теории волн доказывается, что такой цуг должен представлять пакет монохроматических волн с частотами в интервале от ω до ω + Δω (или с волновыми числами от k до k+ Δ k), причем

 

(81.1)

 

Это соотношение справедливо для любых волновых процессов.

Для волны де Бройля — микрочастицы, движущейся вдоль оси x с импульсом p

откуда

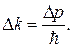(81.2)

 

Подставляя формулу (81.2) в неравенство (81.1), получаем

 

(81.3)

 

В неравенстве (81.3) Δ x — интервал координат, в котором локализована движущаяся микрочастица, описываемая волной де Бройля; Δ p — интервал, в котором заключен импульс микрочастицы. Формулу (81.3) называют соотношением неопределенностей Гейзенберга. Оно показывает, что координата x микрочастицы и ее импульс p не имеют одновременно значений, равных x и p. Их значения определены лишь с некоторой степенью точности. Другими словами, классические понятия координаты и импульса применимы к микрочастицам лишь в пределах, устанавливаемых соотношением Гейзенберга (81.3).

Возникает вопрос, почему в классической физике соотношение (81.3) не играет никакой роли и движущаяся макрочастица имеет определенные значения координаты и скорости? В качестве примера рассмотрим пылинку массой 10–13 кг и размером 1 мкм = 10–6 м, координата которой определена с точностью до 0,01 ее размера, т. е. . Согласно формуле (81.3),

откуда

Легко сообразить, что эта неопределенность скорости практически не сказывается при всех скоростях, с которыми движется такая макрочастица. Поэтому, в отличие от квантовой механики, в классической механике применимы понятия координаты и скорости.

 

Пример 81.1. Определить относительную неопределенность 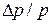импульса движущейся частицы, если неопределенность ее координаты равна длине волны де Бройля.

 

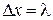
Дано:     Решение
–?

 

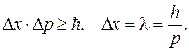
Ответ:

 

Пример 81.2. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, локализованного в области размером l = 0,2 нм.

Дано:   l = 0,2 нм   Решение    
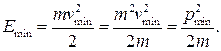
E min–?

Ответ:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)