 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Скорость и ускорение
Мы уже говорили, что при движении частицы ее радиус-вектор меняется в общем случае как по модулю, так и по направлению. В кинематике вводят величину, характеризующую быстроту изменения радиуса-вектора со временем. Ее называют скоростью  частицы.
частицы.
Пусть в момент времени 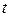 частица, двигаясь по траектории, находилась в точке 1 (рис. 2.1). За элементарный (очень малый) промежуток времени
частица, двигаясь по траектории, находилась в точке 1 (рис. 2.1). За элементарный (очень малый) промежуток времени  радиус-вектор частицы получит элементарное приращение
радиус-вектор частицы получит элементарное приращение 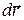 . Векторную величину
. Векторную величину 
 (2.1)
(2.1)
называют скоростью частицы в точке 1 траектории. Вектор  направлен, так же как и вектор
направлен, так же как и вектор 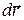 , по касательной к траектории в точке 1.
, по касательной к траектории в точке 1.

Рис. 2.1
Аналогично определяют скорость частицы в любой точке траектории или, что то же самое, в любой момент времени 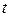 движения частицы. В математике правую часть равенства (2.1) называют производной радиуса-вектора по времени. Следовательно, скорость v частицы в момент времени
движения частицы. В математике правую часть равенства (2.1) называют производной радиуса-вектора по времени. Следовательно, скорость v частицы в момент времени  равна производной по времени от радиуса-вектора этой частицы. Очевидно, для определения скорости частицы в любой момент времени надо знать закон движения частицы (1.3).
равна производной по времени от радиуса-вектора этой частицы. Очевидно, для определения скорости частицы в любой момент времени надо знать закон движения частицы (1.3).
Можем написать
 (2.2)
(2.2)
где  — проекции вектора
— проекции вектора  на координатные оси.
на координатные оси.
Модуль скорости
 (2.3)
(2.3)
Принимая во внимание соотношения (1.7) и (2.1), можем записать выражение для элементарного пути, проходимого частицей за элементарный (очень малый) промежуток времени  :
:
 (2.4)
(2.4)
где v — модуль скорости.
Чтобы определить путь S 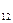 , проходимый частицей за промежуток времени
, проходимый частицей за промежуток времени 
 , надо просуммировать элементарные пути
, надо просуммировать элементарные пути 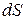 по длине отрезка траектории, проходимой частицей за этот промежуток времени. В математике такую операцию называют интегрированием. Можем написать
по длине отрезка траектории, проходимой частицей за этот промежуток времени. В математике такую операцию называют интегрированием. Можем написать


 (2.5)
(2.5)
Путь, проходимый частицей за промежуток времени  равен определенному интегралу от функции v (t), взятому в пределах от
равен определенному интегралу от функции v (t), взятому в пределах от  , до
, до  . Очевидно, чтобы произвести интегрирование (2.5), надо знать зависимость модуля скорости частицы от времени
. Очевидно, чтобы произвести интегрирование (2.5), надо знать зависимость модуля скорости частицы от времени 

При движении частицы ее скорость может меняться как по модулю, так и по направлению. В кинематике вводят величину, характеризующую быстроту изменения скорости со временем. Ее называют ускорением 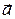 частицы.
частицы.
Пусть в момент времени  частица, двигаясь по траектории, находилась в точке 1 (рис. 2.2).
частица, двигаясь по траектории, находилась в точке 1 (рис. 2.2).

Рис. 2.2
За элементарный (очень малый) промежуток времени 
 скорость частицы получит элементарное приращение
скорость частицы получит элементарное приращение  . Векторную величину
. Векторную величину
 (2.6)
(2.6)
называют ускорением частицы в точке 1 траектории. Вектор 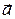 направлен так же, как и вектор
направлен так же, как и вектор  .
.
Аналогично определяют ускорение частицы в любой точке траектории или, что то же самое, в любой момент времени 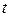 движения частицы. Ускорение
движения частицы. Ускорение 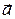 частицы в момент времени
частицы в момент времени 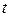 равно производной по времени от скорости этой частицы.
равно производной по времени от скорости этой частицы.
Очевидно, зная закон движения частицы (1.3), можно найти зависимость скорости  от времени
от времени 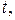 а затем ускорение
а затем ускорение  в любой момент времени.
в любой момент времени.
Можем написать
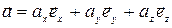 , (2.7)
, (2.7)

где  — проекции вектора
— проекции вектора 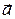 на координатные оси.
на координатные оси.
Модуль ускорения
 (2.8)
(2.8)
Проведем через некоторую точку траектории частицы две оси: ось τ, направленную по касательной к траектории в сторону вектора  , и ось
, и ось 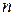 , направленную по нормали к траектории к центру кривизны траектории в одной точке (центру окружности, дугой которой является элементарный (очень малый) отрезок траектории частицы в районе данной точки) (рис. 2.3). Тогда вектор
, направленную по нормали к траектории к центру кривизны траектории в одной точке (центру окружности, дугой которой является элементарный (очень малый) отрезок траектории частицы в районе данной точки) (рис. 2.3). Тогда вектор 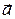 можно представить в виде суммы двух составляющих
можно представить в виде суммы двух составляющих  и
и  :
:
 , (2.9)
, (2.9)
где 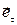 и
и  — орты осей
— орты осей  и
и 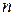 ;
;  и
и  — проекции векторов
— проекции векторов  и
и  на эти оси.
на эти оси.  Вектор
Вектор  называют касательной или тангенциальным ускорением, вектор
называют касательной или тангенциальным ускорением, вектор  — нормальным ускорением.
— нормальным ускорением.

Рис. 2.3
Можно показать, что проекция
 (2.10)
(2.10)
производной по времени от модуля скорости частицы. Тангенциальное ускорение частицы характеризует быстроту изменения модуля ее скорости. При ускоренном движении вектора  совпадает с направлением скорости
совпадает с направлением скорости  частицы. При замедленном движении вектор
частицы. При замедленном движении вектор  противоположен направлению скорости
противоположен направлению скорости  .
.
Можно показать, что проекция
 |
(2.11)
где R — радиус кривизны траектории в данной точке. Нормальное ускорение характеризует быстроту изменения направления скорости частицы. Вектор  всегда направлен к центру кривизны траектории.
всегда направлен к центру кривизны траектории.
Модуль ускорения
 . (2.12)
. (2.12)
Пример 2.1. Радиус-вектор при движении частицы по траектории изменяется по закону 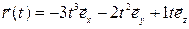 , м. Найти модуль
, м. Найти модуль 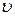 скорости частицы в момент t 1 = 2с.
скорости частицы в момент t 1 = 2с. 

Дано:
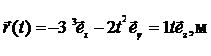

| Решение
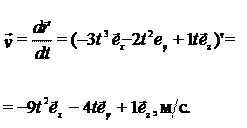
|
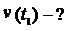
|


Ответ: 
Пример 2.2. Закон движения частицы  м. Найти проекцию
м. Найти проекцию  ускорения частицы в момент времени t 1 = 5c.
ускорения частицы в момент времени t 1 = 5c.
Дано:

 
| Решение


|

|

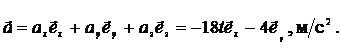
 .
.
 .
.
Ответ: ax (t 1) = – 90 м/с2.
Пример 2.3. В момент времени  скорость частицы
скорость частицы 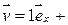
 ускорение
ускорение  Найти радиус кривизны R траектории в той точке, в которой частица находится в момент времени
Найти радиус кривизны R траектории в той точке, в которой частица находится в момент времени  .
.
Дано:

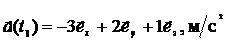
| Решение



 . .
|


Ответ: 
Пример 2.4. Закон движения частицы  Найти путь
Найти путь 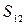 частицы за одиннадцатую секунду ее движения.
частицы за одиннадцатую секунду ее движения.



Дано:



| Решение

|

|


Ответ: S 12 = 63 м.
Поиск по сайту: