 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Закон Ома для проводника
Ом экспериментально установил закон, согласно которому сила тока, протекающего по металлическому проводнику, пропорциональна разности потенциалов на его концах (напряжению U):
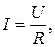 (44.1)
(44.1)
где R — электрическое сопротивление (или просто сопротивление) проводника. Сопротивление измеряют в омах (Ом). Оно зависит от формы и размеров проводника, а также от материала проводника и его температуры.
Сопротивление однородного цилиндрического проводника
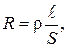 (44.2)
(44.2)
где ℓ — длина проводника; S — площадь его поперечного сечения; ρ — коэффициент, называемый удельным электрическим сопротивлением (или просто удельным сопротивлением) проводника. Удельное сопротивление проводника измеряют в ом-метрах (Ом·м). Оно зависит от материала проводника и его температуры.
Величину σ, обратную удельному сопротивлению, называют удельной электрической проводимостью (или просто удельной проводимостью) проводника. Ее измеряют в сименсах на метр (См/м). Сименс — единица измерения, обратная ому (1 См = 1 Ом–1).
Соотношение (44.1) называют законом Ома для проводника в интегральной форме. Найдем дифференциальную форму этого закона. Для этого выделим мысленно в окрестности некоторой точки проводника элементарный объем в виде цилиндра высотой d ℓ и площадью основания dS с образующими, параллельными векторам 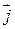 и
и  в этой точке (рассмотрим изотропный проводник, в котором направления плотности тока
в этой точке (рассмотрим изотропный проводник, в котором направления плотности тока 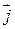 и напряженности
и напряженности  электрического поля совпадают) (рис. 44.1).
электрического поля совпадают) (рис. 44.1).
 Рис. 44.1
Рис. 44.1
| Для такого элементарного цилиндра имеем
 (44.3) (44.3)
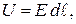 (44.4) (44.4)
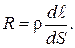 (44.5) (44.5)
|
Подставляя формулы (44.3)–(44.5) в соотношение (44.1), получаем
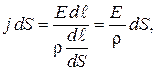
откуда
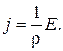
Так как векторы 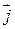 и
и  имеют одинаковое направление, можно написать
имеют одинаковое направление, можно написать
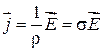 (44.6)
(44.6)
— плотность тока в некоторой точке проводника равна произведению удельной проводимости проводника на напряженность электрического поля в этой точке (закон Ома для проводника в дифференциальной форме).
Поиск по сайту: