|
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Затухающие колебания
Если частица движется в вязкой среде, то кроме силы упругости на нее действует сила сопротивления среды
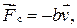 (11.1)
(11.1)
где  — положительная постоянная;
— положительная постоянная;  — скорость частицы.
— скорость частицы.
Согласно основному уравнению динамики частиц,
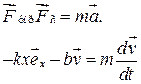
или в проекциях на ось 
 (11.2)
(11.2)
Учитывая, что 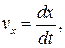 перепишем выражение (11.2) в виде дифференциального уравнения
перепишем выражение (11.2) в виде дифференциального уравнения
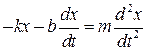
или
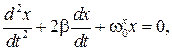 (11.3)
(11.3)
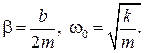
Решение уравнения (11.3) дает закон движения частицы
 (11.4)
(11.4)
где 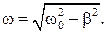
Из выражения (11.4) видно, что амплитуда  колебаний частицы не является постоянной величиной, уменьшается со временем
колебаний частицы не является постоянной величиной, уменьшается со временем 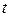 по экспоненциальному закону
по экспоненциальному закону
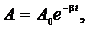 (11.5)
(11.5)
где 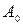 — положительная постоянная, являющаяся амплитудой колебаний в момент
— положительная постоянная, являющаяся амплитудой колебаний в момент 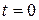 , поэтому носит название начальной амплитуды колебаний частицы (рис. 11.1)
, поэтому носит название начальной амплитуды колебаний частицы (рис. 11.1)
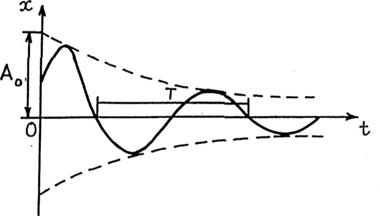
Рис. 11.1
Следовательно, колебанияе частицы в вязкой среде не являются гармоническими. Их называют затухающими колебаниями частицы.
Положительные постоянные β и ω называют соответственно коэффициентом затухания и круговой частотой колебаний частицы. Постоянная величина  является круговой частотой колебаний при отсутствии силы сопротивления (при
является круговой частотой колебаний при отсутствии силы сопротивления (при  ). Ее называют собственной частотой колебаний частицы.
). Ее называют собственной частотой колебаний частицы.
Быстроту убывания амплитуды  колебаний частицы характеризуют величиной, называемой логарифмическим декрементом затухания
колебаний частицы характеризуют величиной, называемой логарифмическим декрементом затухания
 |
(11.6)
где Т — период колебаний (промежуток времени, за который повторяются нулевые значения координаты  частицы). Так как
частицы). Так как
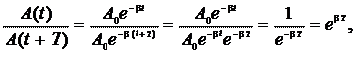 |
получаем
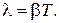 (11.7)
(11.7)
Пример 11.1. Закон движения частицы 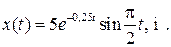 Найти модуль v скорости частицы в момент времени
Найти модуль v скорости частицы в момент времени  где T — период колебаний частицы.
где T — период колебаний частицы.
Дано:
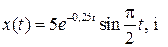
 
| Решение
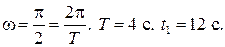
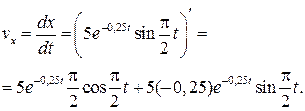
|
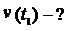  
|

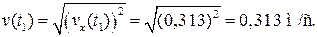
Ответ: 
Пример 11.2. Амплитуда колебаний частицы за время 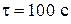 уменьшилась в 2,7 раз. Чему равен коэффициент затухания β?
уменьшилась в 2,7 раз. Чему равен коэффициент затухания β?
Дано:
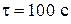
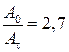
| Решение

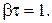
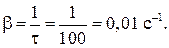
|
| β –? |
Ответ: 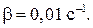
Пример 11.3. Амплитуда колебаний частицы уменьшилась в 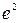 раз за
раз за  колебаний. Чему равен логарифмический декремент затуханий λ?
колебаний. Чему равен логарифмический декремент затуханий λ?
Дано:
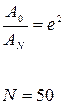
| Решение
 
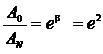
где τ — время, в течение которого произошли
| ||
| λ –? |
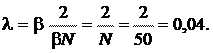
Ответ: 
Поиск по сайту:
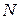 колебаний частицы
колебаний частицы