Вынужденные колебания. Вынужденными называются колебания, которые возникают в системе под действием постоянно действующей внешней силы

Вынужденными называются колебания, которые возникают в системе под действием постоянно действующей внешней силы, которая изменяется по периодическому закону, например,

, (3.19)

где – амплитуда вынуждающей силы, – ее круговая частота. Тогда второй закон Ньютона запишется в виде

.

В скалярном виде . Пусть сила трения равна нулю , тогда

, (3.20)

разделив уравнение (3.20) на m, и перенося члены с х в левую часть, получим дифференциальное уравнение

(3.21)

это неоднородное дифференциальное уравнение 2-го порядка для вынужденных колебаний, поэтому его решение имеет следующий вид:

. (3.22)

При действии вынуждающей силы тело будет колебаться с частотой вынуждающей силы. Значение амплитуды в уравнении (3.22) определяется следующим образом:

.

Рисунок 3.9

Видно, что амплитуда колебаний зависит не только от амплитуды вынуждающей силы, но и от разности квадратов собственной частоты и частоты вынуждающей силы. Графически эта зависимость представлена на рисунке 3.9. Отдельные кривые на графике соответствуют различным значениям параметра (коэффициента затухания), чем меньше , тем выше и правее лежит максимум данной кривой.

При частоте колебаний вынуждающей силы равной частоте собственных колебаний системы 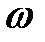₀ () амплитуда колебаний резко возрастает, т.е. . Это явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты вынуждающей силы с собственной частотой системы называется резонансом. В реальных условиях наличие трения ограничивает возрастание амплитуды. С увеличением трения уменьшаются и амплитуда колебаний, и резонансная частота.

Резонанс может быть как полезным, так и вредным явлением. Вредное действие резонанса связано с изменениями, которые он может вызвать, например, действие инфразвука на внутренние органы человека. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания.

3.8 Механические волны

Процесс распространения колебаний в среде называется волной. Распространение механических колебаний в среде объясняется наличием силовых связей в веществе. Частицы среды, в которой распространяется волна, не переносятся волной, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны, поэтому чаще всего продольные волны представляют собой распространения сжатия или растяжения (например, пружины), сгущения или разряжения. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных направлению распространения волны (например, если дергать за закрепленную за один конец веревку, то по ней будут распространяться поперечные волны).

Распространяясь от источника колебаний волновой, процесс охватывает все новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к данному моменту времени, называется фронтом волны. Таким образом, фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченного в волновой процесс. Фронт волны все время перемещается в пространстве, оставаясь перпендикулярным распространению волны.

Рисунок 3.10

Возьмем точечный источник колебаний и рассмотрим распространение колебаний, вызванных этим источником в однородной, изотропной среде. Очевидно, что в этом случае колебания будут распространяться во всех направлениях с одинаковой скоростью, то фронт волны будет иметь форму сферы, такую волну называют сферической (см. рисунок 3.10).

Если фронт волны представляет собой плоскость, то волну называют плоской.

Уравнением волны называется зависимость смещения колеблющейся точки от координат и времени:

.

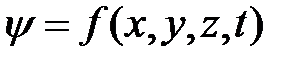Рассмотрим одномерную волну, т.е. волну, распространяющуюся лишь вдоль оси х. Каждая точка среды совершает гармонические колебания, которые можно описать законом:

.

До точки с произвольной координатой х возмущение дойдет через время , равное , где – скорость распространения волны. Следовательно, колебания этой точки будут запаздывать. Уравнение бегущей волны будет отличаться от уравнения колебаний, и для плоской одномерной волны будет иметь вид:

. (3.23)

Величина представляет собой смещение любой из точек среды с координатой в некоторый фиксированный момент времени (предполагается, что потерь энергии в среде нет, тогда амплитуда у всех точек одинакова). Выражение называется фазой волны. Поскольку функция является периодической функцией, то фаза волны повторяется через . График зависимости, представленный уравнением (3.23) представляет как бы моментальную фотографию смещений колеблющихся точек волны в данный момент времени (см. рисунок 3.11).

Рисунок 3.11 Черта между верхушками

Расстояние между двумя ближайшими точками, колеблющимися в одинаковых фазах, называется длиной волны и обозначается .

Периодом волны называется время одного полного колебания ее точек.

Скорость волны определяется скоростью распространения колебаний от одной точки среды к другой. Скорость распространения волны связана с длиной волны и периодом следующим образом: .

3.9. Звук

Понятие звука обычно ассоциируется у нас со слухом и, следовательно, с физиологическими процессами в ушах, а также с психологическими процессами в нашем мозгу (там происходит переработка ощущений, поступающих в органы слуха). Кроме того, под звуком мы понимаем физическое явление, вызывающее действие на наши уши, а именно продольные волны.

При рассмотрении звука можно выделить три основных аспекта. Во-первых, должен существовать источник звука; причем, как и для любой другой волны, источником звуковой волны являются колебания тела. Во-вторых, энергия переносится от источника звука в виде продольных звуковых волн, и, в-третьих, звук регистрируется (воспринимается) нашим ухом или прибором.

Мы обычно считаем, что звук распространяется в воздухе, потому что, как правило, именно, воздух контактирует с нашими барабанными перепонками, и его колебания заставляют совершать эти перепонки колебания. Однако звуковые волны могут распространяться и в других веществах. Удары двух камней друг о друга пловец может слышать, находясь под водой, поскольку колебания передаются уху водой. Если приложить ухо к земле, то можно услышать приближение поезда или трактора. В этом случае земля не воздействует непосредственно на ваши барабанные перепонки. Однако продольную волну, распространяющуюся в земле, называют звуковой волной, поскольку ее колебания приводят к колебаниям воздуха во внешнем ухе. Действительно, продольные волны, распространяющиеся в любой материальной среде, часто называют звуковыми. Очевидно, звук не может распространяться в отсутствие вещества. Например, нельзя услышать звон колокола, находящегося внутри сосуда, из которого откачан воздух.

Скорость звука в различных веществах имеет разные значения. В воздухе при температуре 0°С и давлении 1атм звук распространяется со скоростью 331,3 м/с. Скорость звука зависит от модуля упругости и плотности вещества. В жидкостях и твердых телах, которые значительно менее сжимаемы и, следовательно, имеют достаточно большие модули упругости, скорость распространения звука соответственно больше, чем в газах.

Частоты колебаний звуковых волн лежат в пределах от 16 Гц до 20000 Гц. Если частоты колебаний ниже 16 Гц, то такие волны называют инфразвуком, выше 20000 Гц – ультразвуковые волны.

3.10 Особенности инфразвуков и ультразвуков

1 Опыт показывает, что инфразвуковые волны затухают слабо. Поэтому ослабление инфразвуковой волны вызвано только перераспределением энергии по возрастающему фронту волны, если волна близка к сферической. Если же источником является ветровое волнение моря, где длина фронта волны составляет сотни метров, то здесь интенсивность инфразвуковой волны мало меняется с расстоянием. По-видимому, у рыб и морских животных имеется чувствительность к инфразвукам, благодаря чему они чувствуют приближение, шторма. Мощные инфразвуковые волны, возникающие при шторме, практически без затухания распространяются в море на расстояния в сотни и тысячи километров и сигнализируют о его приближении.

2. Ультразвуковые волны отличаются от обычного слышимого звука большой частотой колебаний, поэтому длина волны ультразвука значительно меньше длины волны звука. Благодаря малой длине волны, ультразвуковые волны не дифрагируют (раздел 11.3). Поэтому они могут быть получены в виде направленных пучков, подобных пучкам света. Отражение и преломление ультразвуковых волн происходит по законам аналогичным законам отражения и преломления света (раздел 10.1).

Интенсивность ультразвуковой волны пропорциональна квадрату амплитуды волны и квадрату частоты колебаний, поэтому ультразвуковые волны имеют большую интенсивность. Высокая частота позволяет получить волны с интенсивностями до 100 Вт/см²=10 кВт/м². При таких больших интенсивностях ультразвуковая волна влияет на свойства вещества и ход технологических процессов. Если в жидкости распространяется ультразвук большой интенсивности, то большие напряжения в моменты разряжения могут приводить к образованию пустот, т.е. к разрывам жидкости. Это явление называется кавитацией. Развитию кавитации способствуют пузырьки газа, всегда имеющиеся в жидкостях. Огромное давление, которое развивается, когда захлопывается кавитационный пузырек, можно использовать для дробления и размельчения различных веществ. После обработки ультразвуком размеры частиц твердого тела, находящегося в жидкости, существенно уменьшаются, и смесь (суспензия) становится более однородной. Помещая, ультразвуковой преобразователь в сосуд, в котором находятся две несмешивающиеся жидкости (например, вода и масло), получим через некоторое время однородную эмульсию с размерами частиц от долей микрометра до нескольких микрометров. Этот эффект может быть использован для получения новых типов лекарств путем создания водной эмульсии нерастворимых лекарственных веществ.

Действие ультразвука существенно ускоряет процессы, связанные с проникновением жидкости в пористые среды, что в свою очередь ускоряет многие химические и технологические процессы.

Также в медицине при помощи ультразвука осуществляют сварку сломанных костей, диагностические исследования и т.д. Биологическое действие ультразвука (приводящее к гибели микробов) позволяет использовать его для стерилизации лекарственных веществ, а также медицинских инструментов.

Поиск по сайту: