Геометрическая оптика

10.1 Законы геометрической оптики

Длины воспринимаемых глазом световых волн очень малы (порядка 10^-7м). Поэтому, отвлекаясь от волновой природы света, его распространение можно в первом приближении рассматривать вдоль некоторых линий, называемых лучами. В предельном случае, соответствующем , законы можно сформулировать на языке геометрии. В соответствии с этим раздел оптики, в котором пренебрегают конечностью длин волн, называется геометрической оптикой.

Основу геометрической оптики образуют четыре закона: 1) закон прямолинейного распространения света; 2) закон независимости световых лучей; 3) закон отражения света; 4) закон преломления света.

Изотропной средой называется такая среда, свойства которой во всех направлениях оказываются одинаковыми. В таких средах свет во всех направлениях распространяется с одной и той же скоростью. Если в среде нет никаких вкраплений, то среда называется однородной изотропной.

Закон прямолинейного распространения света утверждает, что в однородной изотропной среде свет распространяется прямолинейно.

Закон независимости световых лучей утверждает, что лучи при пересечении не взаимодействуют друг с другом. Пересечение лучей не мешает каждому из них распространяться независимо друг от друга.

При падении светового луча на границу раздела двух сред образуются лучи отраженный и преломленный (см. рис.10.1).

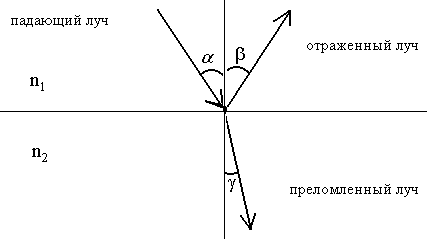Рисунок 10.1

Закон отражения света утверждает, что отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром восстановленным в точку падения А; угол отражения b равен углу падения a.

Закон преломления света формулируется следующим образом: преломленный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точку падения А; отношение синуса угла падения a к синусу угла преломления g есть величина постоянная для данных двух сред

. (10.1)

Величина n ₁₂ называется относительным показателем преломления второй среды относительно первой

, (10.2)

где n ₁ и n ₂ – абсолютные показатели преломления среды 1 и 2 соответственно.

Абсолютный показатель преломления показывает во сколько раз скорость распространения света в среде u меньше скорости распространения света в вакууме с.

.

10.2 Закон полного внутреннего отражения

Заменив в формуле (10.1) n ₁₂ выражением (10.2), закон преломления можно представить в виде

. (10.3)

Из формулы (10.3) видно, что при переходе света из оптически более плотной среды в оптически менее плотную (n ₁> n ₂) преломленный луч света удаляется от нормали к поверхности раздела двух сред, т.е. угол g больше угла a. Увеличение угла падения a сопровождается более быстрым ростом угла преломления g и, при достижении углом a значения

, (10.4)

угол g становится равным p/2. Угол падения, при котором угол преломления равен p/2, называется предельным углом падения. Если угол падения a будет больше предельного угла падения a _пред,, то наблюдается явление полного внутреннего отражения: луч света, падающий на границу раздела двух сред полностью отражается обратно в первую среду, а преломление прекращается.

Рисунок 10.2

Рисунок 10.2а

Таким образом, для того, чтобы наблюдалось явление полного внутреннего отражения необходимо осуществление двух условий: 1) луч должен переходить из среды оптически более плотной в среду оптически менее плотную; 2) угол падения должен быть больше значения предельного угла падения.

На измерении предельного угла падения основано устройство рефрактометров – приборов для определения показателя преломления жидкостей. В медицине рефрактометры применяются для определения концентрации веществ в растворе (например, позволяют контролировать качество приготовления лекарственных препаратов).

Рисунок 10.3.

Явление полного внутреннего отражения лежит в основе волоконной оптики. Свет, попадая внутрь прозрачного волокна, окруженного веществом с меньшим показателем преломления, многократно отражается от боковой поверхности волокна и распространяется вдоль этого волокна. Диаметр этих тонких стеклянных или пластиковых волокон может быть доведен до нескольких микрометров. Для передачи больших световых потоков и сохранения гибкости светопроводящей системы отдельные волокна собираются в пучки (жгуты) – световоды. Рисунок 10.3 демонстрирует, как распространяется свет по тонкому волокну, испытывая только скользящие отражения от стенок, т.е. полное внутреннее отражение. Если световоду придать сложную форму, то угол падения обычно превышает предельный, и свет будет передан от одного торца световода до другого практически без ослабления. Этот эффект используется в декоративных светильниках и при подсветке струй в фонтане. Световоды можно использовать для освещения труднодоступных мест, например, внутренних органов человека. Вводя через пищевод больного световод, врач получает возможность визуально обследовать стенки желудка. По одним волокнам посылается свет для освещения желудка, а по другим идет отраженный свет. На противоположном торце световода наблюдатель видит серию светлых и темных пятен (как на телевизионном экране), т.е. картину у противоположного торца световода. Волокна должны быть оптически изолированы друг от друга. Обычно на них наносится вещество с меньшим показателем преломления. Волокна должны быть строго параллельны, иначе изображение не получится четким. Чем больше волокон в световоде и чем они тоньше, тем лучше разрешаются детали изображения.

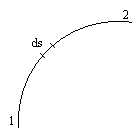Рисунок 10.4

10.3 Принцип Ферма

В основу геометрической оптики может быть положен принцип Ферма. Из этого принципа вытекают законы прямолинейного распространения, отражения и преломления света. В формулировке самого Ферма принцип гласит, что свет распространяется по такому пути, для прохождения которого ему требуется минимальное время.

Для прохождения прямолинейного участка пути d s (cм. рис.10.4) свету требуется время , где – скорость распространения света в данной среде. Заменив через с / n, получим, что . Следовательно, время t, затрачиваемое светом на прохождение пути от точки 1 до точки 2, равно . Имеющая разность длины величина называется оптической длиной пути. В однородной среде оптическая длина пути равна произведению геометрической длины пути s на показатель преломления среды n: . Пропорциональность времени прохождения t оптической длине пути L дает возможность сформулировать принцип Ферма следующим образом:

свет распространяется по такому пути, оптическая длина которого минимальна.

Линзы

Прозрачное тело, ограниченное двумя сферическими поверхностями, называется линзой (см.рис.10.5).

Рисунок 10.5

Прямую линию, на которой лежат центры сферических поверхностей, образующих линзу, называют главной оптической осью линзы. Главная оптическая ось линзы пересекает сферические поверхности в точках М и N – это вершины линзы. Если расстоянием MN можно пренебречь по сравнению с R ₁ и R ₂, то линза называется тонкой. В этом случае точка М совпадает с точкой N, и тогда точка М будет называться оптическим центром линзы (см.рис.10.5).

Точка, в которой собираются линзой лучи от бесконечно удаленного источника (бесконечно удаленный источник дает параллельный пучок лучей), называется фокусом линзы. Плоскость, проходящая через фокус перпендикулярно к главной оси, называется фокальной плоскостью. Расстояние от оптического центра линзы до фокуса называется фокусным расстоянием. F. Его величина определяется соотношением

(10.5)

где n-относительный показатель преломления материала линзы, d – расстояние от объекта до линзы, f - расстояние от линзы до изображения. Эта общая формула линзы применяется для выпуклых и вогнутых линз при любом расположении источника. Нужно только принять во внимание знаки d, f, R₁ и R₂. Знаки определяются следующим образом:

1. Радиус кривизны считается положительным, если свет падает на выпуклую поверхность, и отрицательным, если свет падает на вогнутую поверхность.

2. Расстояние от объекта до линзы d положительно, если расстояние измеряется по ходу луча, в противном случае оно отрицательно;

3. Расстояние от линзы до изображения f положительно, если расстояние измеряется по ходу луча, в противном случае оно отрицательно

В зависимости от знака и величины R₁ и R₂, а также от знака (n-1) фокусное расстояние F может быть положительным или отрицательным, соответственно фокус называют действительным или мнимым. Если фокусы действительны, параллельные лучи после преломления в линзе сходятся и линза называется собирающей (рис.10.6,а). При мнимых фокусах параллельные лучи после преломления в линзе становятся расходящимися. Поэтому такие линзы называются рассеивающими или отрицательными (рис. 10.6,б).

рис.10.6,а. рис.10.6,б.

Если материал линзы преломляет сильнее, чем окружающая среда (например, стеклянная линза в воздухе), то собирающими будут линзы двояковыпуклые.

Виды линз показаны на рисунках 10.7,а и 10.7,б. Первая группа линз, находящихся в воздухе, это собирающие линзы. На рисунке 10.7,б показаны линзы, которые в воздухе пучки света будут рассеивать.

рис.10.7,а. рис.10.7,б.

Если материал, из екоторого изготовлены линзы, преломляет меньше, чем окружающая среда (например, воздушная полость в воде), то линзы вида 10.7,а будут рассеивающими, а вида 10.7,б собирающими.

Величину обратную фокусному расстоянию называют оптической силой линзы. Оптическую силу измеряют в диоптриях. Оптической силой в 1 диоптрию обладает линза фокусным расстоянием 1 м:

(10.6

Поиск по сайту: