Колебания пружины

Рисунок 3.3

Простейшим примером гармонического колебания, служат колебания груза на конце пружины. Многие другие виды колебательных движений проявляют большое сходство с этими колебаниями; например, колебания, происходящие в системе кровообращения, дыхания, сокращения мышц. Поэтому мы разберем этот пример подробно. Будем считать, что массой пружины можно пренебречь и, что пружина установлена горизонтально, как показано на рисунке 3.3.

К одному концу пружины прикреплен груз массой m, который движется без трения по горизонтальной поверхности. Любая пружина имеет определенное значение длины, при котором с ее стороны на груз не действует сила; в этом случае говорят, что пружина находится в положении равновесия. Если сдвинуть груз вправо, растягивая пружину, или влево, сжимая ее, то пружина действует на груз с силой, которая стремится вернуть его в положение равновесия; такую силу называют возвращающей. Для нашей системы возвращающая сила прямо пропорциональна расстоянию ,на которое сжимается или растягивается пружина (см. рисунок 3.3):

. (3.4)

Знак минус означает, что возвращающая сила всегда противоположна по направлению перемещению . Если на рисунке 3.3 мы направим ось, например, вправо, заметим, что положение равновесия мы выбрали в точке 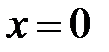. Когда пружину сжимают, сила направлена вправо (см. рисунок 3.3), а перемещение влево. Постоянная величина в формуле (3.4), называется жесткостью пружины.

Что же произойдет, если пружину растянуть на длину , и затем отпустить? Пружина действует на груз с силой, которая стремится вернуть его в положение равновесия. Но поскольку эта сила сообщает грузу ускорение, груз приходит в положение равновесия со значительной скоростью. Заметим, что в положении равновесия сила, действующая на груз, уменьшается до нуля, а скорость его в этой точке максимальна (см. рисунок 3.2). Когда груз, проскочив положение равновесия, движется влево, сила со стороны пружины замедляет его, и в точке груз на мгновение останавливается, а затем начинает двигаться в противоположном направлении, пока не придет в точку 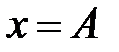, откуда он начал движение. Затем весь этот процесс повторяется. Рассматриваемый колебательный процесс происходит лишь под действием внутренней силы – силы упругости, поэтому рассматриваемые колебания являются собственными.

Уравнение второго закона Ньютона для груза на пружине имеет вид:

.

Преобразуем это уравнение следующим образом:

. (3.5)

Коэффициент при положителен, поэтому его можно представить в следующем виде:

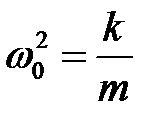. (3.6)

Применяя в уравнении (3.5) обозначения (3.6), получим:

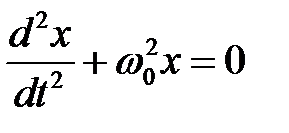. (3.7)

Таким образом, движение груза под действием силы вида (3.4) описывается линейным, однородным дифференциальным уравнением второго порядка.

Легко убедиться, что общее решение уравнения (3.7) имеет вид:

. (3.8)

Смещение изменяется со временем по закону косинуса. Следовательно, движение системы, находящейся под действием силы , представляет собой гармоническое колебание. Из уравнения (3.8) следует, что введенный коэффициент 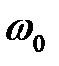представляет собой частоту колебаний и называется собственной частотой колебаний системы, находится по формуле

. (3.9)

Из формулы (3.9), очевидно, что частота собственных колебаний системы определяется свойствами самой системы, т.е. ее упругими свойствами.

3.4 Полная энергия собственных колебаний

В простых гармонических колебаниях происходит непрерывный переход потенциальной энергии в кинетическую энергию, и обратно; полная энергия колеблющейся системы сохраняется, если в системе отсутствуют силы трения.

Выясним, как изменяется со временем кинетическая и потенциальная энергия гармонического колебания на примере упругой пружины. Кинетическая энергия равна (см. выражения (2.18) и (3.2))

. (3.10)

Потенциальная энергия выражается формулой (см. выражения (2.21) и (3.1))

. (3.11)

Складывая (3.9) (3.10), с учетом соотношения (3.6) получим:

(3.12)

Из соотношения (3.12) видно, что полная энергия свободных колебаний равна максимальной потенциальной энергии или максимальной кинетической энергии гармонических колебаний и прямо пропорциональна массе колеблющейся точки , квадрату амплитуды 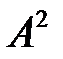и квадрату частоты колебания.

Поиск по сайту: