Условия минимумов и максимумов интерференции

Анализируя уравнение (11.2), мы пришли к выводу, что при значении 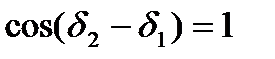наблюдается усиление интенсивности, поэтому условие кратности разности фаз 2 p

(11.3)

называется условием максимума интенсивности, а условие

(11.4)

– условием минимума интенсивности.

Обычно эти условия формулируются не через разность фаз, а через оптическую разность хода волн , так как разность фаз трудно измерить.

Рассмотрим понятие оптической разности хода. Пусть S ₁ и S ₂ источники света (см. рис. 11.3). В точке Р экрана волны, идущие от этих источников накладываются, при этом первая волна проходит геометрический путь S ₁ P, а вторая путь S ₂ Р, если волны распространяются в воздухе, то разность хода находится так , если волны распространяются в различных средах, то разностью хода называют разность между оптическим ходом первого луча и второго (см принцип Ферма, раздел 10.3), где n ₁ и n ₂ показатели преломления соответствующих сред.

Разность хода и разность фаз связаны соотношением

(11.5)

отсюда видно, что при разности фаз равной p , разность хода интерферирующих волн равна половине длине волны l /2.

Тогда условия максимумов интерференции можно сформулировать следующим образом:

максимальное усиление результирующего колебания наступает, если оптическая разность хода слагаемых волн равна четному числу длин полуволн, т.е.

(11.6)

– условие максимума; аналогично формулируется условие минимумов:

ослабление результирующего колебания будет, если оптическая разность хода слагаемых волн равна нечетному числу длин полуволн, т.е.

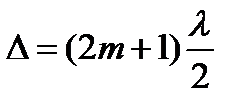(11.7)

– условие минимума, где m = 0,1,2,……называется порядком интерференционного максимума или минимума (см. рис.11.3а).

Таким образом, интерференционная картина представляет собой чередование минимумов и максимумов интенсивности (см. рис.11.3а)..

Шириной интерференционной полосы называют расстояние между двумя ближайшими максимумами или минимумами.

рис.11.3а

11.2.3 Интерференция в тонких пленках

Наиболее типичным и распространенным примером интерференции света в природе является интерференция в тонких пленках: мыльные пузыри, радужная пленка нефти на воде и интерфереционнные пленки на стеклах очков для того, чтобы погасить отраженные лучи и т.д.

При падении световой волны на тонкую прозрачную пластинку (или пленку), имеющую показатель преломления n, происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые могут интерферировать (см. рис.11.4). Интерференционная картина будет наблюдаться на экране, расположенном в фокальной плоскости линзы. В этом случае мы будем вести речь об интерференции в отраженных лучах.

Рисунок 11.4

Разность хода, приобретаемая лучами, до того как они сойдутся на экране, если прозрачная пластинка находится в воздухе, равна

. (11.8)

При вычислении оптической разности хода необходимо учесть изменение фазы волны при отражении. В точке А (см. рис.11.4) отражение происходит от границе раздела среды, оптически менее плотной, со средой оптически более плотной. Поэтому фаза вектора напряженности электрического поля претерпевает изменение на p. Из уравнения (11.5) следует, что в этом случае ход световой волны отраженной от верхней грани пластинки увеличивается на половину длины волны (l/2). Тогда, оптическая разность хода световых волн, отраженных от верхней и нижней граней пластинки, будет выглядеть следующим образом:

. (11.9)

Если в выражении (11.9) величины АВ и ВС выразить через толщину прозрачной пластинки, найти значение величины АD из треугольника АСD, то оптическую разность хода можно найти следующим образом:

, (11.10)

где d – толщина прозрачной пластинки, a – угол падения луча света на первую грань.

Интерференция на тонких пленках представляет интерес при использовании контактных линз. Между контактной линзой и роговицей глаза может возникнуть воздушная прослойка. При отражении света в тонкой воздушной прослойке наблюдается интерференционная картина, она имеет вид концентрических колец, получивших название колец Ньютона.

С помощью интерференции на тонких пленках можно определять толщину очень тонких пленок и их показатель преломления.

Поиск по сайту: