Понятие потока вектора напряженности. Теорема Гаусса

Под потоком вектора напряженности понимают количество силовых линий, пронизывающих площадку , расположенную перпендикулярно силовым линиям. На рисунке 5.7 однородное электростатическое поле, изображенное параллельными силовыми линиями, проходит через площадку . Если площадка не перпендикулярна силовым линиям, то берут ее проекцию (на рисунке 5.7 изображена пунктиром). Для однородного электростатического поля поток вектора напряженности вычисляется следующим образом:

. (5.5)

Рисунок 5.7

Рассмотрим теперь более общий случай, когда электростатическое поле неоднородно. В этом случае поверхность разобьем на элементов, площади которых обозначим . Разбиение должно быть таким, чтобы электрическое поле в пределах элемента было однородным. Тогда поток напряженности через всю поверхность будет суммой 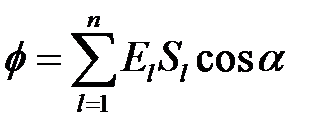. В пределе сумма переходит в интеграл по всей поверхности:

. (5.6)

Поток считается положительным, если направление вектора напряженности совпадает с направлением нормали проведенной к площадке 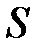, и отрицательным, если направление вектора напряженности противоположно направлению нормали.

Возьмем точечный заряд и посчитаем поток вектора напряженности поля, созданного этим зарядом, через любую замкнутую поверхность, внутри которой находится этот заряд (см. рисунок 5.8). Точечный заряд создает неоднородное поле, поэтому поверхность нужно подобрать таким образом, чтобы интеграл (5.6) был простым, для этого нужно значение подобрать равным 1. Согласно рисунку 5.8 этой поверхностью может быть сфера, в центре, которой, и расположен точечный заряд. Тогда выражение (5.6) приобретает следующий вид:

. (5.7)

На любой выбранной поверхности сферы значение вектора напряженности одинаково по величине (см. (5.3)) во всех точках сферы. Поэтому величину 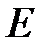можно вынести за знак интеграла:

Рисунок 5.8

. Интеграл , где 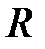– радиус выбранной сферы. Таким образом, поток через сферу

. (5.8)

Из выражения (5.3) подставим значение напряженности электростатического поля для точечного заряда в формулу (5.8) и окончательно получаем, что поток через сферу пропорционален заряду, находящемуся внутри этой сферы:

.

Если внутри сферы находится несколько точечных зарядов, то можно записать выражение потока следующим образом:

. (5.9)

Полученное выражение носит название теоремы Гаусса, которая читается следующим образом:

поток вектора напряженности электростатического поля через любую замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой замкнутой поверхности, деленной на .

Теорема Гаусса справедлива для потока вектора напряженности электростатического поля через любую замкнутую поверхность; она утверждает, что если поток, направленный внутрь поверхности, не равен потоку, направленному наружу, то это обусловлено наличием зарядов внутри поверхности.

Теорема Гаусса позволяет в ряде случаев найти напряженность поля гораздо более простыми средствами, чем с использованием принципа суперпозиции полей. Продемонстрируем возможности теоремы Гаусса на следующем примере.

Пусть положительный заряд равномерно распределен по поверхности бесконечной плоскости. Электростатическое поле, созданное равномерно заряженной плоскостью является однородным. Заряд, приходящийся на единицу площади, называется поверхностной плотностью заряда и обозначается

.

Выберем в качестве поверхности интегрирования небольшой цилиндр, ось которого перпендикулярна заряженной плоскости и который пересекается с этой плоскостью (см. рисунок 5.9). Цилиндр - это и есть любая замкнутая поверхность, внутри которой должен быть заряд, создающий поле. Обычно поверхность интегрирования стремятся выбрать так, чтобы напряженность электрического поля была постоянна по всей поверхности, или, по крайней мере, на определенных ее участках, поэтому цилиндр для данного поля является самой подходящей поверхностью интегрирования.

Рисунок 5.9

В силу симметрии следует ожидать, что вектор по обе стороны плоскости перпендикулярен ей и постоянен в пределах торца цилиндра площадью (поле однородно). Поскольку векторы напряженности 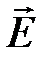не пересекают боковую поверхность цилиндра, то поток через боковую поверхность равен нулю. Потоки через основания цилиндра одинаковы и каждый из них равен . По теореме Гаусса

,

где 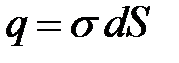– заряд, заключенный внутри цилиндра. Напряженность электрического поля, созданного бесконечной равномерно заряженной плоскостью равна

. (5.10)

Поле двух равномерно заряженных плоскостей. Поле двух параллельных бесконечных плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плотностью 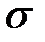, можно найти как суперпозицию полей, создаваемых каждой из плоскостей в отдельности (см. рисунок 5.10). В области между плоскостями складываемые поля имеют одинаковое направление, так что результирующая напряженность равна

. (5.11)

Рисунок 5.10

Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю.

Таким образом, поле оказывается сосредоточенным между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению; следовательно, поле однородно. Линии напряженности представляют собой совокупность параллельных, равноотстоящих друг от друга прямых.

Поиск по сайту: