Связь между напряженностью электростатического поля и потенциалом

Электростатическое поле можно описать либо с помощью векторной величины 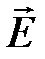(напряженность электростатического поля), либо с помощью скалярной величины (потенциал электростатического поля). Очевидно, что между этими величинами должна существовать определенная связь.

В разделе 5.6 было установлено, что работа сил электростатического поля на элементарно малом отрезке перемещения равна 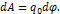С другой стороны эта же работа равна , если перемещать пробный заряд вдоль силовых линий. Приравниваем эти выражения и получаем:

.

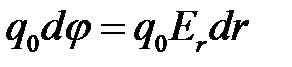Отсюда следует, что напряженность можно выразить через потенциал следующим образом:

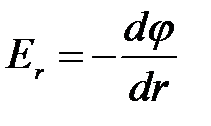, (5.15)

производная, стоящая в правой части равенства, выражает быстроту изменения потенциала в направлении . Мы видим, что проекция вектора напряженности на данное направление равна быстроте изменения потенциала в этом направлении с обратным знаком. Знак минус в выражении (5.15) указывает на то, что вектор напряженности электростатического поля всегда направлен в сторону убыли потенциала.

Для однородного электростатического поля выражение (5.15) выглядит следующим образом:

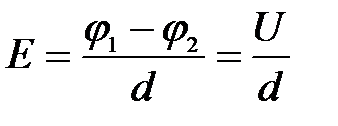, (5.15а)

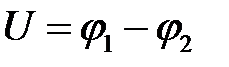где – расстояние между двумя эквипотенциальными поверхностями с потенциалами и , соответственно, – называется напряжением.

Поскольку электростатическое поле можно изобразить графически с помощью силовых линий и эквипотенциальных поверхностей, то необходимо выяснить, как они располагаются по отношению друг к другу. Выберем однородный участок поля, и на этом участке будем перемещать пробный заряд q₀ вдоль эквипотенциальной поверхности. Перемещая пробный заряд, совершаем работу против сил электростатического поля

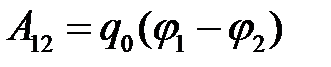, (5.16)

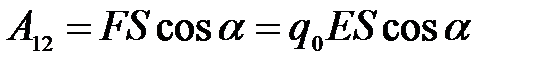. (5.17)

Поскольку пробный заряд перемещается по эквипотенциальной поверхности, то во всех точках этой поверхности потенциалы равны, т.е. 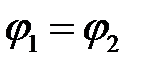, значит по формуле (5.16) получается, что совершаемая работа равна нулю 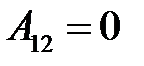. В формуле (5.17) левая часть уравнения также равна нулю, следовательно, в правой части уравнения должен быть равен нулю один из членов. Нулю может быть равен лишь косинус угла 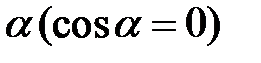, следовательно, угол 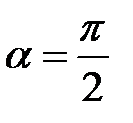. Угол 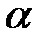– это угол, между перемещением S и направлением действия силы 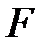, направление которой совпадает с направлением силовых линий. Перемещение пробного заряда происходит по эквипотенциальной поверхности, поэтому можно утверждать, что силовые линии и эквипотенциальные поверхности взаимно перпендикулярны (угол ).

На рисунке 5.4 показаны эквипотенциальные поверхности (точнее, их пересечения с плоскостью чертежа) для поля точечного заряда, которые представляют собой окружности. Так как напряженность электростатического поля 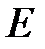самая большая вблизи заряда, то эквипотенциальные поверхности при приближении к заряду тоже становятся гуще.

Рисунок 5.12

Для однородного электростатического поля эквипотенциальные поверхности представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению силовых линий поля (см. рисунок 5.12). При заданном направлении силовых линий электростатического поля потенциал эквипотенциальных поверхностей 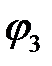является наименьшим.

5.8 Конденсаторы

Конденсатор – это устройство для накопления зарядов. Конденсаторы бывают плоские, цилиндрические, сферические и т.д. Плоский конденсатор состоит из двух разноименно заряженных близкорасположенных плоскостей.

Основной характеристикой конденсатора является его емкость, под которой понимают величину численно равную заряду, который нужно сообщить обкладкам конденсатора, чтобы изменить разность потенциалов между обкладками конденсатора на единицу

. (5.18)

Емкость измеряется в Фарадах [1 Фарад] = [1Кл/В].

Величина емкости определяется геометрией конденсатора (формой и размерами обкладок и величиной зазора между ними), а также диэлектрическими свойствами среды, заполняющей пространство между обкладками конденсатора. Найдем формулу для емкости плоского конденсатора. Если площадь обкладки S, а заряд на ней q, то напряженность поля между обкладками равна

.

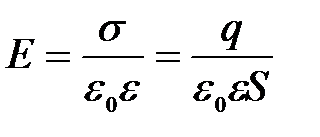(см. формулу (5.11)); 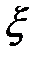– диэлектрическая проницаемость среды, заполняющей зазор между обкладками.

Так как поле между обкладками конденсатора является однородным, то в соответствии с (5.15а) разность потенциалов между обкладками равна

.

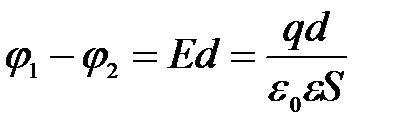Отсюда для емкости плоского конденсатора получается формула:

,

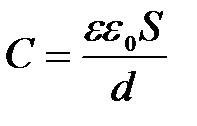где 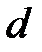– расстояние между обкладками конденсатора, S – площадь обкладок.

Нужно отметить, что клеточная мембрана представляет собой плоский конденсатор.

Вычислим энергию заряженного конденсатора. Для этого представим себе, что конденсатор разряжается, и обозначим через U мгновенное значение напряжения на его обкладках в процессе разряда. Если малое количество заряда dq уходит в процессе разряда с обкладок конденсатора, то работа электрических сил dA (см. раздел 5.6)

,

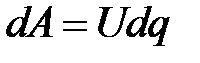выражая в этой формуле заряд обкладок q через напряжение по формуле (5.18), получим

.

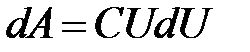Полную работу, совершенную электрическими силами за все время разряда, равную энергии конденсатора W, получим, интегрируя это выражение между значениями напряжения U (начало разряда) и 0 (конец разряда):

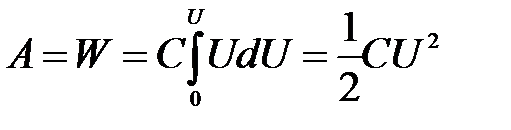. (5.19)

5.9 Энергия электростатического поля

Опыты показывают, что энергия конденсатора сосредоточена в электростатическом поле. Учитывая это можно преобразовать выражение (5.19) для энергии конденсатора таким образом, чтобы в него входила характеристика поля – напряженность.

Рассмотрим однородное поле плоского конденсатора, емкость которого определяется 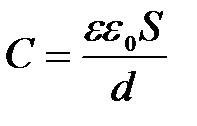, подставим это выражение в формулу (5.19) получим

.

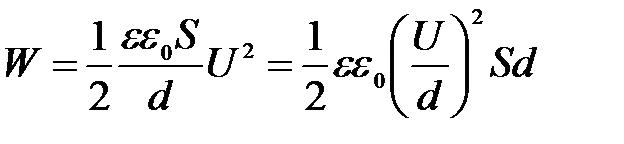Здесь U/d – напряженность электростатического поля Е, а Sd = V – объем, занимаемый полем. Таким образом, энергия однородного поля пропорциональна занимаемому полем объему. Поэтому целесообразно говорить об объемной плотности энергии электростатического поля, т.е. энергии, сосредоточенной в единице объема. Она равна:

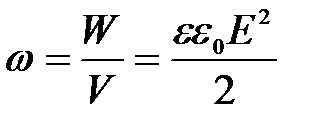. (5.20)

Если электростатическое поле неоднородно, то его всегда можно разбить на элементарные объемы dV и считать, что в пределах этого малого объема поле однородно. Поэтому энергия, заключенная в объеме поля dV будет равна 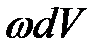. Полная энергия любого электростатического поля может быть представлена в следующем виде:

(5.21)

причем интегрирование производится по всему объему V, где имеется электростатическое поле.

Поиск по сайту: