Дифракция Фраунгофера на одной щели

Пусть на очень длинную прямоугольную щель ширины b падает по нормали к ней плоская световая волна. Если экран расположен бесконечно далеко от щели или за щелью находится линза, направляющая на экран пучки параллельных лучей, то наблюдается дифракция Фраунгофера. Поместим за щелью собирающую линзу, а в фокальной плоскости линзы экран (см. рис.11.6):

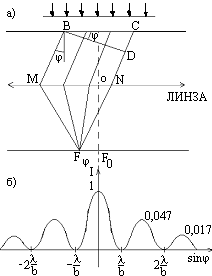Рисунок 11.6

Согласно принципу Гюйгенса элементарные участки открытой части фронта волны являются источниками вторичных волн, распространяющихся в разных направлениях. Линза будет собирать лучи, идущие под углами j в одной точке экрана, под углами j ₁ в другой точке экрана и т.д.. Лучи, пришедшие в точку Р экрана, являются когерентными и интерферируют. Разобьем открытую часть волновой поверхности на зоны параллельные краям щели так, чтобы разность хода лучей от краев соседних зон до точки наблюдения была равна половине длины световой волны l /2. Колебания, приходящие в точку наблюдения от каждой пары соседних зон взаимно гасят друг друга, т.к. находятся в противофазе. Разность хода лучей, идущих от краев щели равна (b-ширина щели) Если для точки наблюдения Р разность хода лучей равна четному числу длин полуволн l /2, то амплитуда колебаний в этой точке равна нулю.

Таким образом, условием минимума является равенство разности хода лучей от краев щели четному числу полуволн или целому числу длин волн

, (11.11)

где m = 1, 2, 3,...

Если для точки Р разность хода равна нечетному числу полуволн, число зон Френеля будет нечетным, действие одной из них окажется не скомпенсированным и наблюдается максимум интенсивности.

В случае, когда угол дифракции равен нулю (j = 0), все колебания оказываются в одной фазе, поэтому в центре экрана наблюдается светлая полоса, соответствующая максимуму нулевого порядка. Интенсивность этого максимума наибольшая.

При

наблюдаются минимумы соответственно 1-го, 2-го и. т.д. порядков.

При

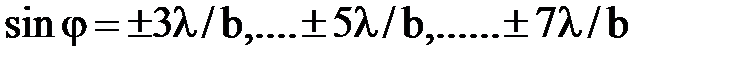
наблюдаются максимумы 1-го, 2-го и т.д. порядков. График зависимости интенсивности света от угла дифракции изображен на рисунке 11.6, на котором указано и соотношение интенсивностей максимумов. За единицу принята интенсивность центрального максимума.

11.3.4 Дифракционная решетка

Современные фармацевтические лаборатории не обходятся без спектрального анализа лекарственных препаратов. При этом виде анализа используют разложение белого света на составляющие его цвета (красный, желтый, зеленый и т.д.) Хорошей разрешающей способностью обладают спектральные приборы, в которых разложение осуществляется с помощью дифракционных решеток.

Рисунок 11.7

Дифракционной решеткой называется совокупность большого числа N отстоящих друг от друга на одном и том же расстояние щелей (см. рис.11.7). Расстояние между серединами соседних щелей d называется периодом решетки (см. рис.11.8). Выясним характер дифракционной картины, получающейся на экране при падении на решетку параллельных световых волн.

Каждая из щелей дифракционной решетки даст на экране дифракционную картину, описываемую графиком, приведенным на рисунке 11.6.

Картины от всех щелей придутся на одно и то же место экрана. Если бы колебания, приходящие в точку P от различных щелей были некогерентными, результирующая картина от N щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в N раз. Однако, колебания от различных щелей будут интерферировать между собой. Поэтому

дифракционная картина от дифракционной решетки будет иной, чем от одной щели.

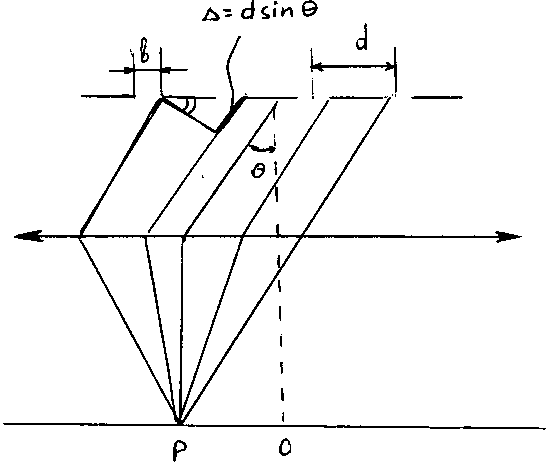Рисунок 11.8

Проанализируем распределение интенсивности в этой картине. Для нахождения интенсивности в каждой точке экрана мы должны найти результирующую амплитуду колебаний в этой точке.

(11.12

где A _i – результирующая амплитуда волн, идущих от каждой отдельной щели.

Для направлений, удовлетворяющих условию минимума для каждой отдельной щели (11.11), все амплитуды A _i =0, поэтому и амплитуда результирующего колебания в соответствующей точке экрана будет равна нулю. Таким образом, условие минимума (11.11) для одной щели является также условием минимума для дифракционной решетки

. (11.13)

Условие (11.13) называют условием главных минимумов. На рисунке 11.8 видно, что разность хода лучей от соседних щелей равна 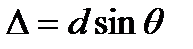. Если разность хода D равна целому числу длин волн, колебания от отдельных щелей приходят в точку наблюдения в фазе и суммарная амплитуда колебаний в соответствующей точке экрана равна 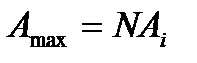. Поэтому условием главных максимумов является

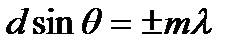. (11.14)

Число m указывает порядок главного максимума. В центре экрана образуется самый интенсивный максимум нулевого порядка, по обе стороны от него располагаются главные максимумы, первого, второго и т.д. порядков. В направлениях, определяемых формулой (11.14), при отдельных значениях m могут и не возникать максимумы. Это будет в направлениях, для которых каждая отдельная щель решетки имеет минимум. Допустим 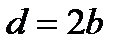, тогда условие появления главного максимума 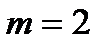имеет вид 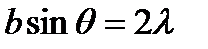или 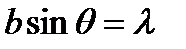, т.е. переходит в условие минимума (11.13). Отсюда следует, что в этом случае все главные максимумы четных порядков не появятся.

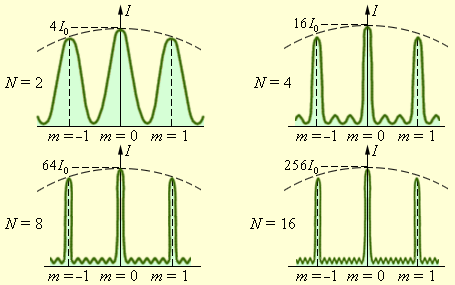
Рисунок 11.9

На рисунке 11.9 представлено распределение интенсивности при дифракции монохроматического света на решетках с различным числом щелей. I₀ – интенсивность колебаний при дифракции света на одной щели. Анализируя приведенные на рисунках дифракционные картины, можно заметить, что в случае двух щелей между главными максимумами располагается один минимум. При росте числа щелей на дифракционной решетке, между соседними максимумами будет расти число минимумов. Кроме того, количество щелей N определяет световой поток через решетку. Чем их больше, тем большая энергия переносится волной через нее. Следовательно, максимумы будут более узкими и более интенсивными (см.рис.11.9). Из формулы (11.14) следует, что лучи различной длины волны, будут иметь максимумы в различных направлениях. Поэтому если на дифракционную решетку падает белый свет, то решетка разложит его, и на экране увидим дифракционный спектр, обращенный к центральной белой полосе (нулевой максимум) фиолетовым концом (см.рис.11.10).

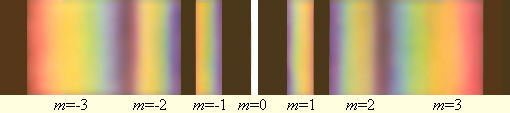Рисунок 11.10

Период дифракционной решетки d связан с числом штрихов, приходящимся на единицу длины решетки n соотношением

.

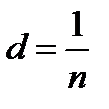Исходя из условий максимума (11.14) для спектра первого порядка длина волны определяется следующим уравнением 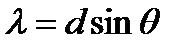, т.е. по углу отклонения лучей, соответствующих той или иной спектральной линии, если известен период дифракционной решетки d, можно найти длину световой волны. Совокупность длин волн или спектр излучения (или поглощения) позволяет делать заключение о химическом, а иногда и изотопном составе вещества.

11.3.5 Разрешающая способность дифракционной решетки

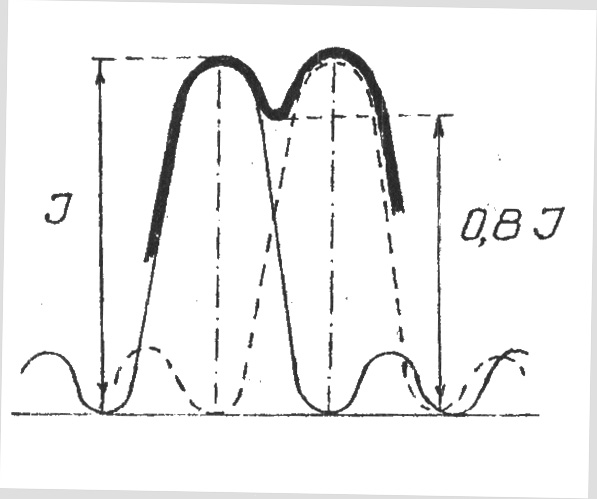Рисунок 11.11

Важной характеристикой дифракционной решетки является разрешающая способность – способность разделить две соседние линии спектра

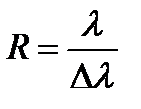, (11.15)

где D l – разница длин волн линий спектра, которые можно еще различить. Релей доказал, что две линии различимы, если центр максимума одной из них приходится на середину минимума другой. В этом случае интенсивность света в промежутке между линиями не превышает 80% от интенсивности в центре линии (см.рис.11.11).

Тогда разрешающая способность дифракционной решетки определится соотношением:

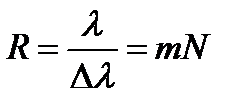. (11.16)

Из этого уравнения следует, что разрешающая способность тем больше, чем больше щелей в решетке и увеличивается с увеличением порядка спектра m,но при этом уменьшается интенсивность линий.

11.4 Поляризация света

Все свойства поляризованного света указывают на то, что его используют для изучения анизотропии веществ. Результаты взаимодействия поляризованного света с любой анизотропной средой содержит информацию об этой анизотропии. Среди элементарных биологических объектов можно найти очень большое число примеров анизотропии. Поляризационнооптическими методами получены ценные сведения о нуклеиновых кислотах и нуклеопротеидах. Изучение дихроизма их растворов в электрических полях дало информацию о дипольных моментах, геометрии, гибкости. С помощью дихроизма изучалась жесткость двойной спирали ДНК в зависимости от внешних условий (температуры, концентрации и др.). Оказалось, что этим способом можно замечать малые изменения структуры ДНК при ультрафиолетовом и рентгеновском облучении, при воздействии ультразвуком. Дихроизм в потоке вирусов, протекающем через узкий капилляр, дает информацию об их внутренней структуре, в частности об упаковке протеинов и укладке цепей ДНК.

Широко применяется исследование двойного лучепреломления при искусственной ориентации сред, в частности ориентации частиц в потоке жидкости. В качестве характерного примера можно привести исследование структуры фаговых частиц, в частности упаковки ДНК в фагах.

11.4.1 Естественный и поляризованный свет

Электромагнитная волна является волной поперечной и представляет собой процесс распространения в пространстве переменных электрических и магнитных полей, которые описываются взаимно перпендикулярными векторами напряженности электрического поля Е и магнитного поля Н (см. рис.11.12а).

Рисунок 11.12

Вектор колеблется в направлении оси, вдоль которой совершает колебания атом или молекула, излучающая свет. В природе свет излучается множеством атомов, поэтому имеется множество отдельных волн, векторы напряженности электрического поля 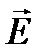, которых колеблются по всем возможным направлениям. Световой пучок, в котором различные направления вектора равновероятны, называется естественным. В естественном свете плоскость колебаний вектора 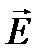(а, следовательно, и вектора 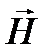) в непрерывно меняется. Если направление света перпендикулярно плоскости рисунка, то схематически естественную волну можно изобразить, как показано на рисунке 11.12б.

Любой вектор можно разложить на составляющие вдоль взаимно перпендикулярных осей. Выберем плоскость перпендикулярную направлению распространения естественного света и систему координат на ней и мысленно спроектируем на оси х и у все возможные положения вектора 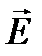, а затем просуммируем все его х -компоненты и все у -компоненты. Очевидно, что для естественного света эти две суммы всегда, при любой ориентации системы координат, будут равны (см. рис.11.13).

Рисунок 11.13

Тогда луч естественного света можно изобразить с помощью этих компонент следующим образом (см. рис.11.14)

Рисунок 11.14

Стрелочками изображаются колебания вектора 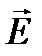, совершающиеся в плоскости рисунка, а точками – колебания вектора 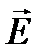,совершающиеся перпендикулярно плоскости рисунка.

Свет, в котором колебания вектора 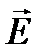подчиняются некоторой закономерности, называется поляризованным. Если колебания вектора 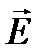происходятв однойплоскости, то волна называется плоско поляризованной или линейно поляризованной, ее схематическое изображение показано на рисунке 11.15.

Рисунок 11.15

Рисунок 11.16

Если же колебания вектора совершаются так, что его конец описывает круг или эллипс, то свет называется поляризованным по кругу или эллиптически поляризованным (см. рис.11.16).

Свет, в котором колебания одного направления преобладают над колебаниями других направлений, называется частично поляризованным. Такой свет можно рассматривать, как смесь естественного света и линейно поляризованного.

Плоскость, в которой колеблется световой вектор в линейно поляризованной волне, мы будем называть плоскостью колебаний. Плоскостью поляризации по историческим причинам называют плоскость, в которой колеблется вектор .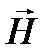

11.4.2 Способы получения поляризованного света. Поляризация при двойном лучепреломлении

Во многих прозрачных средах скорость распространения света одинакова по всем направлениям, так как во всех направлениях одинакова относителоная диэлектрическая проницаемость среды. Такие среды называются изотропными, но в некоторых кристаллах и растворах скорость распространения света в различных направлениях неодинакова. Такие среды называются анизотропными. Анизотропными средами являются, например, кристаллы кварца и исландского шпата, дерево (свойства дерева различны вдоль и поперек ствола). В случае анизотропной среды, показатель преломления различен для различных направлений колебаний вектора 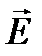световой волны, поэтому при освещении кристалла исландского шпата узким пучком естественного света в кристалле возникают два луча. Один из этих лучей удовлетворяет обычному закону преломления и лежит в одной плоскости с падающим лучом и нормалью к преломляющей поверхности. Этот луч называют обыкновенным (о). Для другого луча, называемого необыкновенным (e), закон преломления света не выполняется (см. рис.11.17).

Рисунок 11.17

Необыкновенный луч не лежит в одной плоскости с падающим лучом и нормалью к преломляющей поверхности. Об анизотропных кристаллах говорят, что они двоякопреломляющие.

В двоякопреломляющих кристаллах существует направление, в котором отсутствует двойное лучепреломление, т.е. показатели преломления обыкновенного и необыкновенного лучей равны n_e = n ₀, тогда это направление называется оптической осью кристалла. Прямая линия О ₁ О ₂ (см.рис.11.17 является оптической осью кристалла исландского шпата (прямая, соединяющая противоположные телесные тупые углы). Всякое направление в кристалле, параллельное О ₁ О ₂ также является оптической осью этого кристалла. Сечение MO ₁ NO ₂ – главное сечение кристалла, или главная плоскость, которая проходит через оптическую ось и нормаль n, проведенную в точку В падения луча АВ. Но если естественный свет падает на кристалл под углом к оптической оси, то в кристалле наблюдается два преломленных луча. На рисунке 11.17 луч света падает по нормали к поверхности, тогда ход лучей (обыкновенного и необыкновенного) можно изобразить в плоскости главного сечения. Колебания вектора 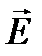в необыкновенном луче BD совершаются в плоскости главного сечения кристалла (луч отмечен черточками), а в обыкновенном луче ВС – в плоскости, перпендикулярной главному сечению (луч отмечен точками). Для необыкновенного луча показатель преломления кристалла n_е зависит от направления луча в кристалле, тогда как n₀ – показатель преломления обыкновенного луча остается постоянным при любом угле падения световой волны на кристалл.

Чтобы использовать такие поляризованные лучи, их нужно отделить один от другого. Это осуществляется в призме Николя. Для изготовления призмы Николя кристалл исландского шпата распиливается по линии AR (см. рис. 11.18) и обе половины склеиваются «канадским бальзамом». Если на николь падает естественный свет, то в призме он раздваивается. Обыкновенный луч, дойдя до слоя канадского бальзама AR, испытывает полное внутреннее отражение от канадского бальзама (см.рис. 11.18), т.к. для обыкновенного луча канадский бальзам оптически менее плотен, чем исландский шпат.

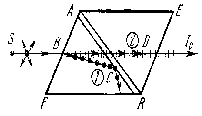
Рисунок 11.18

Таким образом, обыкновенный луч отводится в сторону и поглощается в оправе призмы Николя. Необыкновенный луч 2 свободно проходит через слой канадского бальзама и выходит из призмы полностью поляризованным.

Дихроизм. Существуют кристаллы, которые по-разному поглощают обыкновенный и необыкновенный лучи. Так, если на кристалл турмалина направить пучок естественного света перпендикулярно оптической оси, то при толщине пластинки лишь в несколько миллиметров, обыкновенный луч полностью поглотится, а из кристалла выйдет только необыкновенный луч. Различный характер поглощения обыкновенного и необыкновенного лучей называется анизотропией поглощения или дихроизмом. Дихроизмом в той или иной степени должны обладать все двоякопреломляющие кристаллы, но у разных веществ анизотропия поглощения проявляется по-разному.

Устройства, при помощи которых получают поляризованный свет, называют поляризаторами. Если на пути поляризованного света поместить второй николь, то интенсивность вышедшего света будет зависеть от взаимной ориентации обоих николей. Если их главные плоскости параллельны, то интенсивность прошедшего через оба николя света наибольшая. Если же эти направления перпендикулярны друг другу, то через вторую призму свет не пройдет. Первый николь играет роль поляризатора, второй – анализатора. Совокупность поляризатора и анализатора представляет собой типичную поляризационную установку, позволяющую исследовать различные поляризационные явления в разных средах, помещая их между поляризатором и анализатором.

Поляроиды. Кроме двойного лучепреломления, для поляризации света применяются искусственные пленки – поляроиды; отражение света от диэлектриков; преломление света в стопе стеклянных пластинок и т.д.

11.4.3 Закон Малюса

Если взять два поляроида, один поляроид Р – поляризатор; из него выходит линейно поляризованный свет (вектор 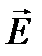колеблется по направлению РР), второй поляроид А – анализатор (колебания вектора происходят по направлению ЛЛ), то по закону Малюса интенсивность света I, выходящего из анализатора, пропорциональна квадрату косинуса угла a между направлением плоскостей колебаний вектора напряженности электрического поля 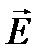волн, прошедших через поляризатор и анализатор, т. е.

(11.17)

где I ₀ – интенсивность линейнополяризованного света, выходящего из поляризатора Р, если – интенсивность естественного света, то

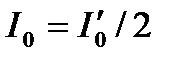(11.18)

Закон Малюса очень легко выводится. Интенсивность света, выходящего из поляризатора, пропорциональна квадрату амплитуды колебаний вектора напряженности, прошедших через поляризатор 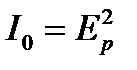, а интенсивность света, выходящего из анализатора, пропорциональна квадрату амплитуды колебаний вектора напряженности 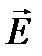, прошедших через анализатор 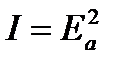. Е _р и Е _а –амплитуды колебаний вектора напряженности 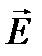, прошедшего анализатор и поляризатор. Из рисунка 11.19 видно, что

. (11.19)

Тогда, чтобы найти интенсивность света прошедшего через анализатор, нужно выражение (11.22) возвести в квадрат, так как интенсивность пропорциональна квадрату амплитуды, в результате получим:

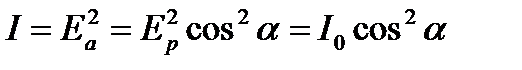(11.20)

Если направления плоскостей колебаний поляризатора и анализатора перпендикулярны, т.е. a =90°, то говорят, что поляризатор и анализатор скрещены (установлены на гашение света – через скрещенные поляризаторы свет не проходит).

Рисунок 11.19

Если направления плоскостей поляризатора РР и анализатора АА совпадают (a =0), то интенсивность проходящего света будет максимальной. Для любого другого угла a интенсивность света вычисляется по формуле (11.20).

11.4.4 Вращение плоскости поляризации

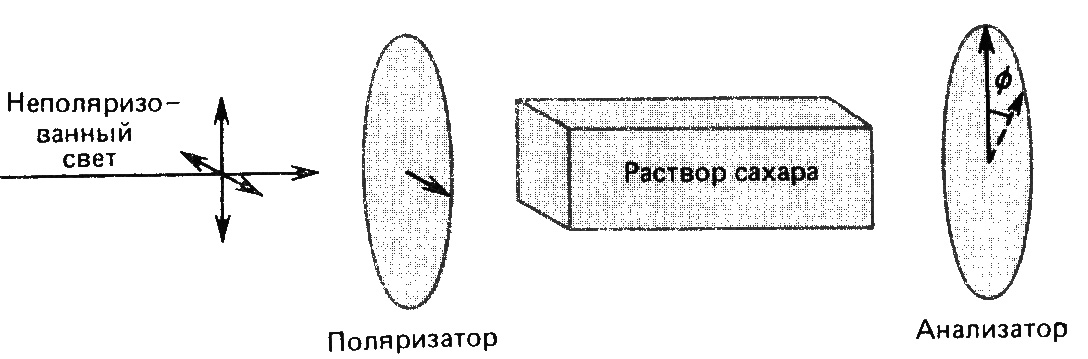Рисунок 11.20

Поставим на пути естественного светового пучка два поляроида так, чтобы их оптические оси были перпендикулярны друг другу («скрещенные» поляроиды) (см.рис.11.20). Свет через эту систему поляроидов не пройдет: первый поляроид превратит естественный свет в линейно поляризованный, который поглотится во втором поляроиде. Поместим теперь на пути светового пучка кювету с раствором сахара. Мы увидим, что поле зрения просветлилось. Повернув поляроид вправо на некоторый угол j, мы опять добьемся полного затемнения поля зрения.

Таким образом, приходим к выводу, что при прохождении пучка линейно поляризованного света через раствор сахара, свет остается линейно поляризованным, но плоскость колебаний и, соответственно, плоскость поляризации повернулись на некоторый угол.

Вещества, вызывающие поворот плоскости поляризации, называются оптически активными. Оптическая активность наблюдается у ряда кристаллических и аморфных тел. В частности, оптически активны кварц, сахар, раствор сахара в воде, скипидар, белки, аминокислоты, гормоны и другие. Оптическая активность веществ обусловлена асимметрией молекул, которые могут иметь форму спиралей, как, например, молекулы некоторых белков. Вещества, поворачивающие плоскость поляризации вправо по ходу луча называются правовращающими. Вещества, поворачивающие плоскость поляризации влево по ходу луча, называются левовращающими. Обычный сахар, декстроза, или D – глюкоза, принадлежит к числу правовращающих веществ. Большинство аминокислот и белков – левовращающие вещества.

Кристаллические вещества сильнее всего вращают плоскость поляризации в случае, когда свет распространяется вдоль оптической оси кристалла. Угол поворота j плоскости поляризации пропорционален пути l, пройденному лучом в кристалле:

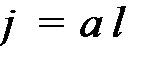, (11.21)

где коэффициент a называют постоянной вращения, она зависит от свойств вещества и зависит от температуры и длины волны, используемого света.

В растворах угол поворота j пропорционален пути луча в растворе d и концентрации активной компоненты вещества С:

. (11.22)

Здесь [ a ] – удельная вращательная способность, численно равная углу поворота на единицу длины пути при концентрации, равной единице. Эта физическая величина зависит от длины волны (как ~ 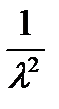), практически не зависит от агрегатного состояния вещества и слабо зависит от температуры.

Численное значение удельной вращательной способности одинаково для двух разновидностей одного и того же оптически активного вещества: правовращающей и левовращающей.

Так как угол вращения j пропорционален концентрации раствора, то оптическая активность служит стандартным методом измерения концентраций растворов оптически активных веществ. Оптическая активность полезна также при определении пространственной структуры больших молекул (например, белков) или ее изменений в различных условиях.

11.4.5 Оптическая активность в живой природе

Оптически активные кристаллы всегда встречаются в виде двух структур, одна из которых является зеркальным изображением другой. Казалось бы, что и органические оптически активные вещества должны существовать в двух подобных состояниях. Между тем опыт показывает, что раствор сахара всегда вращает плоскость поляризации вправо, т.е. по часовой стрелке, если смотреть навстречу лучу. Таким свойством обладает не только сахар, но и все другие продукты органического происхождения: белки, аминокислоты, нуклеиновые кислоты и т.п.

Если изготовить синтетическим путем аналогичное вещество (например, сахар), то оно не будет оптически активным. Синтетически получается смесь, содержащая равное количество право и левовращающих молекул. Вообще в неживой природе все вещества с несимметричными молекулами существуют в виде таких смесей. Если с такой смесью начинает взаимодействовать живое существо, то оно усвоит, лишь одну из структур, соответствующую характеру оптической активности элементов этого существа. Например, если в раствор синтетического сахара поместить бактерии, питающиеся сахаром, то они будут усваивать только правовращающий сахар. Через некоторое время левовращающего сахара в растворе окажется гораздо больше, чем правовращающего, что можно будет обнаружить по повороту плоскости поляризации. Спустя некоторое время бактерии усвоят из смеси весь правовращающий сахар и начнут голодать, хотя в растворе остается еще много левовращающего сахара, но организм живых существ его не усваивает.

Асимметрия оптической активности характерна только для биологического вещества и продуктов органического происхождения. Так, например, тот факт, что у нефти обнаружена оптическая активность, служит веским доводом в пользу теории органическом происхождении нефти.

Причины асимметрии оптической активности у живых существ не вполне ясны. Возможно, что эта асимметрия возникла случайно и затем была закреплена механизмом наследственности.

Проверь себя:

1. Могут ли интерферировать лучи света, идущего от двух настольных ламп?

2. Могут ли интерферировать два любых красных луча?

3. Что вы можете сказать о значении интенсивности света в максимуме интерференции?

4. Что вы можете сказать о значении интенсивности света в минимуме интерференции?

5. Какие физические величины нужно знать, чтобы определить оптическую разность хода?

6. Как связаны между собой оптическая разность хода и разность фаз?

7. Изменится ли положение максимумов интерференционной картины на экране, если в ход одного из интерферирующих лучей вставить стеклянную пластинку?

8. Можно ли поляризовать продольную волну?

9. Чем отличается естественный свет от линейно поляризованного света?

10. Какую роль играет канадский бальзам в призме Николя?

11. Чем анизотропный материал отличается от изотропного материала?

12. Какими свойствами должен обладать кристалл исландского шпата, чтобы быть двоякопреломляющим?

13. Для естественного или поляризованного света выполняется закон Малюса?

14. Всегда ли при прохождении через анизотропный кристалл образуется два луча?

15. Как направлены колебания вектора напряженности электрического поля в обыкновенном луче?

16. Как направлены колебания вектора напряженности электрического поля в необыкновенном луче?

17. Какие вещества называются оптически активными?

18. Почему бывает две разновидности оптически активных веществ?

12.1 Закон Бугера. Поглощение света

Поглощением света называется уменьшение интенсивности света при прохождении через любое вещество вследствие превращения световой энергии в другие виды энергии.

При прохождении световой волны через вещество часть энергии волны затрачивается на возбуждение колебаний электронов. Частично эта энергия вновь возвращается излучению в виде вторичных волн, порождаемых электронами; частично же она переходит в энергию движения атомов, т. е. во внутреннюю энергию вещества. Поэтому интенсивность света при прохождении через вещество уменьшается — свет поглощается в веществе. Вынужденные колебания электронов, а, следовательно, и поглощение света становятся особенно интенсивными при резонансной частоте.

Вывод закона поглощения. Закон поглощения света веществом можно вывести, не рассматривая внутреннего механизма взаимодействия света с веществом. Пусть через однородное вещество распространяется пучок параллельных световых лучей. Выделим в веществе бесконечно тонкий слой dх (см. рис.12.1), ограниченный параллельными поверхностями, перпендикулярными к лучам. Интенсивность при прохождении света сквозь этот слой изменяется на величину – dI (знак «минус» говорит о том, что интенсивность уменьшается).

Рисунок 12.1

Очевидно, dI пропорционально интенсивности I_х, дошедшей до данного слоя, а также толщине слоя вещества dx, т.е.

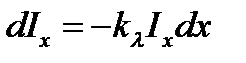. (12.1)

Коэффициент k_l зависит от длины световой волны, падающего света и химической природы поглощающего вещества, и называется коэффициентом поглощения (длина волны излучения связана с частотой l = с / n, с – скорость света). Пусть а – полная толщина слоя вещества, I _о и I – интенсивность световой волны, падающей на вещество и вышедшей из него. Уравнение (12.1) – дифференциальное уравнение с разделяющимися переменными. Перенесем I_х в этом уравнении в левую часть и проинтегрируем полученное выражение

,

,

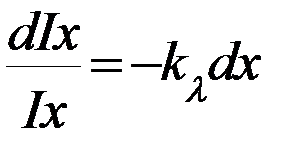в результате получим

или

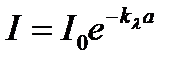. (12.2)

Формула (12.2) носит название экспоненциального закона поглощения света – закон Бугера.

Коэффициент поглощения 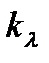– это физическая величина, обратная толщине слоя а, при прохождении которого интенсивность света уменьшается в е раз . Коэффициент поглощения в области видимого света для воздуха равен 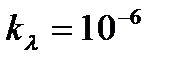см^-1, для воды 2×10^-3см^-1, для металлов 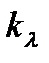имеет порядок десятков тысяч – 10³-10⁴см^-1, поэтому металлы непрозрачны для света.

Большое значение для медицины имеет изучение поглощения света в растворах. В этом случае поглощение зависит также и от концентрации вещества в растворе. Закон поглощения с учетом концентрации раствора, называемый законом Бугера-Ламберта-Бера, записывается в виде:

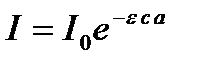, (12.3)

где e – молекулярный коэффициент поглощения (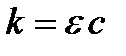), зависящий от природы молекул растворенного вещества, от длины волны попадающего в раствор света и температуры раствора, с – концентрация раствора, а – толщина слоя раствора. Закон Бугера-Ламберта-Бера (13.5) справедлив при условии, что растворитель не поглощает света данной длины волны и раствор имеет невысокую концентрацию. Этот закон справедлив до тех пор, пока сохраняется независимость коэффициента поглощения от интенсивности светового потока.

Для некоторых практических расчетов наиболее удобно выражение закона Бугера (13.3) через десятичные логарифмы

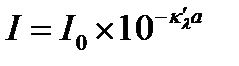. (12.4)

Видно, что коэффициенты 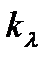и 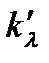cвязаны между собой соотношением: . Произведение 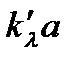– называется оптической плотностью слоя вещества (D), т.е. .

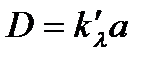Пропусканием (Т) называется отношение интенсивности прошедшего света к интенсивности света падающего I / I _o

.

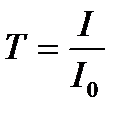Связь оптической плотности и пропускания. Оптическая плотность вещества равна десятичному логарифму от величины, обратной пропусканию света веществом:

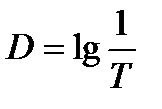. (12.5)

При оптической плотности D = 1 пропускание Т = 0,1 = 10%, при оптической плотности D= 2 пропускание Т = 0,01 = 1% и т.д. с увеличением оптической плотности пропускание света уменьшается по закону, выраженному соотношением (12.5).

Поиск по сайту: