Кинематика материальной точки

Из курса элементарной физики мы знаем, что отношение перемещения ко времени движения называется средней скоростью по перемещению.

Мгновенная скорость движущейся точки соответствует средней скорости движения по перемещению, когда время движения становиться очень малым. Математически это определение можно записать в виде:

.

Таким образом, мгновенную скорость можно определить как производную радиус-вектора движущейся материальной точки по времени:

.

Следует заметить, что мы не положили просто 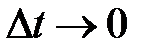, поскольку величина 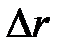при этом также была бы равна нулю и мы имели бы неопределенное число. Таким образом, отношение необходимо рассматривать как единое целое; поскольку мы полагаем 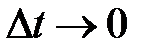, 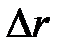также стремится к нулю, однако отношение приближается к некоторому определенному значению, которое и называется мгновенной скоростью.

Модуль вектора скорости можно найти следующим образом:

.

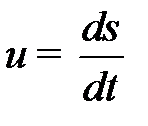Нужно отметить, что скорость – это векторная величина. Вектор мгновенной скорости всегда направлен по касательной к траектории в соответствующей точке (см.рис.1.2).

Рисунок 1.2 Векторы скорости и в моменты времени соответственно

и для частицы на рисунке 1.1.

Можно решить и обратную задачу кинематики, т.е. по заданному значению скорости можно найти путь, пройденный материальной точкой за промежуток времени от до :

.

Величину пройденного пути можно представить как площадь фигуры, которая ограничена кривой зависимости величины скорости от времени .

Нужно отметить, что скорость – это векторная величина. Вектор мгновенной скорости всегда направлен по касательной к траектории в соответствующей точке (см. рисунок 1.2).

Рисунок 1.3 V исправить на u

При неравномерном движении необходимо знать закон изменения скорости со временем. Для этого вводится понятие ускорения. Среднее ускорение – это физическая величина, которая характеризует быстроту изменения скорости со временем: , где и 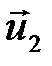– мгновенные скорости в моменты времени и . Как следует из определения, ускорение – это векторная величина, направление которой всегда совпадает с вектором изменения скорости . На рисунке 1.3 изображены векторы мгновенных скоростей в разные моменты времени. Чтобы сравнить эти скорости сделаем параллельный перенос вектора в начало вектора . Тогда вектор изменения скорости 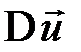будет направлен от конца вектора к концу вектора .

Подобно скорости существует понятие мгновенного ускорения, которое определяется следующим образом:

.

Ускорение материальной точки в данный момент времени, это физическая величина, равная пределу отношения изменения скорости к промежутку времени, за который это изменение произошло, при стремлении промежутка времени к нулю. Математически это определение имеет следующий вид:

.

Запишем вектор скорости через единичный вектор (см. уравнение 1) . Поскольку скорость движения материальной точки – это величина векторная, то ее изменение может происходить как по величине, так и по направлению, поэтому найдем мгновенное ускорение, взяв производную от скорости по времени (находим производную от произведения)

Таким образом, ускорение можно представить суммой двух независимых членов, один из которых определяет изменение скорости по величине, а другой по направлению. Изменение скорости по величине характеризуется тангенциальным ускорением 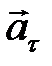, которое направлено по касательной к траектории, т.е. совпадает по направлению со скоростью, а величина тангенциального ускорения находится следующим образом:

.

Изменение скорости по направлению характеризуется нормальным ускорением , которое всегда перпендикулярно вектору скорости и направлено к центру радиуса кривизны траектории, по которой движется материальная точка. Величина нормального ускорения находится по формуле

,

Где – это значение мгновенной скорости в данной точке траектории, а – радиус кривизны траектории.

Полное ускорение материальной точки представляет векторную сумму тангенциального и нормального ускорений

Модуль полного ускорения находится следующим образом:

.

Поиск по сайту: