ПРОВЕРЬ СЕБЯ

1) Что такое колебание?

2) Что называю свободными колебаниями?

3) Что называю вынужденными колебаниями?

4) Что называю гармоническими колебаниями?

5) Дайте определение амплитуды, периода и частоты колебаний.

6) Запишите связь циклической частоты колебаний с периодом колебаний.

7) Дайте определение фазы колебаний.

8) Запишите уравнение смещения колебаний.

9) Как определяются скорость и ускорение гармонических колебаний?

10) Что такое сила упругости?

11) Запишите второй закон Ньютона для груза на пружине.

12) Что называют собственной частотой колебаний?

13) Чему равна полная энергия свободных колебаний?

14) Объясните поведения колебаний при разности фаз равной:

А) нечетному числу p,

Б) четному числу p.

15) Запишите уравнение затухающих колебаний.

16) Что такое коэффициент затухания?

17) Дайте определение и запишите формулу для логарифмического

декремента затухания.

18) При каких условиях движение становится апериодическим?

19) Запишите уравнение для вынужденных колебаний.

20) Что называется резонансом? Какова его роль?

21) Что такое волна?

22) Что называют продольной и поперечной волной? Когда эти волны

возникают?

23) Что такое фронт волны?

24) Что называют уравнением волны?

25) Какую волну называют сферической?

26) Запишите уравнение для плоской одномерной волны.

27) Что называют фазой, скоростью,периодом, частотой волны?

28) Объясните понятие звука.

29) С какой скоростью звук распространяется в воздухе при температуре 0°С и давлении 1атм?

30) Чем отличаются ультразвуковые волны от обычного слышимого звука?

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

4 Жидкости

Общим свойством для жидкостей и газов является их изотропность, т.е. эти среды имеют одинаковые свойства в различных направлениях. Вследствие этого внешнее давление, производимое на жидкость или газ, передается во все стороны равномерно (закон Паскаля).

Различают два основных типа течений жидкостей и газов. Если течение плавное и смежные слои как бы скользят друг относительно друга, то его называют ламинарным или слоистым. Характерная особенность ламинарного течения в том, что каждая частица жидкости (газа) движется по гладкой траектории и траектории разных частиц не пересекаются (рис 4.1,а). Когда скорость течения превышает определенный предел, зависящий от ряда факторов, течение становится турбулентным. Турбулентное течение характеризуется наличием беспорядочных маленьких «водоворотов», называемых вихрями (рис. 4.1,6). Вихри поглощают огромное количество энергии, и, хотя внутреннее трение, называемое вязкостью, существует и в ламинарном течении, в турбулентном течении вязкость оказывается значительно большей. Ламинарное течение легко отличить от турбулентного, капнув в движущуюся жидкость немного чернил или пищевой краски. Как для ламинарного, так и для турбулентного течения можно выделить важнейшие характеристики. 1) Жидкость (газ) можно рассматривать либо как сжимаемую, либо как несжимаемую. 2) Вязкость, или внутреннее трение, имеет место в любом течении жидкости (газа), однако вязкостью тоже часто можно пренебречь. В начале мы будем рассматривать невязкое (идеальное) течение, а затем уже изучим влияние вязкости. 3) Течение может быть установившимся (стационарным). Скорость такого течения в любой точке пространства не изменяется во времени (это не значит, что она не может быть разной в различных точках пространства). Если скорость в данной точке изменяется со временем, то такое течение называется нестационарным;тотечение наблюдается, например, когда мы только что открыли водопроводный кран и потекла вода. Нас будут интересовать главным образом стационарные течения. 4) Течение может быть вихревым и безвихревым (потенциальным). В безвихревом течении полный момент импульса жидкости относительно любой точки равен нулю. Иначе говоря, если бы мы ввели куда-либо в течение, крошечную вертушку с лопастями, то она не стала бы вращаться. Если бы вертушка закрутилась, как в воронке или водовороте, то течение было бы вихревым.

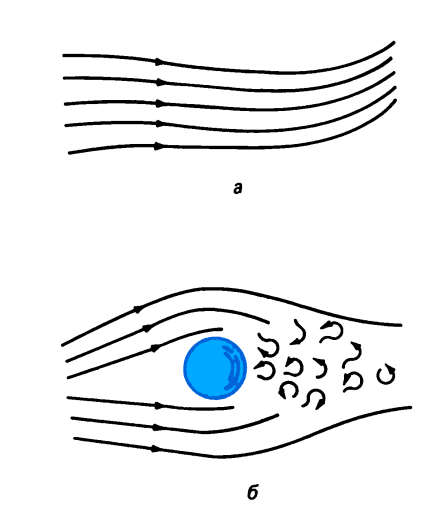Рис. 4.1.а-ламинарное течение; б-турбулентное

течение.

4.1 Линии и трубки тока.

В установившемся ламинарном потоке жидкости (газа) траектория, по которой движется данная частица, называется линией тока (рис. 4.1,а). Скорость жидкости в любой точке направлена по касательной к линии тока (рис. 4.2). Линии тока не пересекаются друг с другом, так как в противном случае в точке их пересечения скорость оказалась бы неоднозначной. Пучок линий тока, такой, как на рис. 4.3, называют трубкой тока.

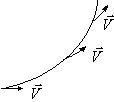Рисунок 4.2

Если вектор скорости в каждой точке пространства с течением времени будет оставаться постоянным, то такое течение жидкости будет стационарным.

Вектор скорости, будучи в каждой точке касательным к линии тока, будет касательным и поверхности трубки тока; следовательно, частицы жидкости при своем движении не пересекают стенок трубки тока. Если за время 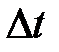в трубку тока вошел объем жидкости , то такой же объем жидкости за такое же время должен выйти из трубки тока.

За промежуток времени 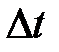переместившиеся объемы жидкости таковы:

,

,

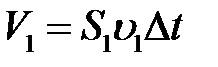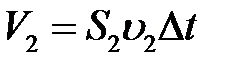Рисунок 4.3

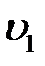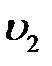где и скорости течения жидкости в сечениях 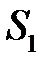и соответственно, поскольку объемы одинаковы , поэтому 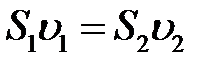. Данное уравнение, выведенное для двух сечений потока несжимаемой жидкости, называется уравнением непрерывности.

В общем случае для идеальной жидкости в стационарных условиях произведение скорости течения жидкости на поперечное сечение трубки тока остается неизменным в любом сечении трубки, т.е. уравнение непрерывности имеет вид

.

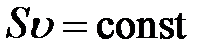Из уравнения непрерывности следует, что в более узких сечениях трубки тока скорость течения жидкости должна быть больше, чем в широких сечениях. Мы знаем, что капиллярное русло в системе кровообращения имеет достаточно большую площадь сечения, поэтому в капиллярном русле скорость течения крови будет, заметно меньше, чем в артериях.

4.3.2 Уравнение Бернулли. Давление в потоке жидкости

В стационарном потоке идеальной жидкости вырежем часть тонкой трубки тока с сечениям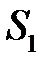и и . Во входном сечении S ₁ давление p ₁, скорость и высота сечения над произвольным уровнем h ₁; в выходном сечении S ₂ соответственно р ₂, , h ₂ (см. рисунок 4.4).

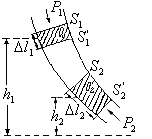Рисунок 4.4

За промежуток времени D t масса входящей в отсек жидкости равна массе жидкости, выходящей из отсека.

Масса жидкости m, протекающей за время D t через сечение S ₁ имеет кинетическую энергию, равную 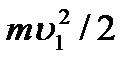, и потенциальную энергию . В результате действия сил давления на сечения S ₁ и S ₂ со стороны слоев жидкости, находящихся слева от S ₁ и справа от S ₂, производится работа

,

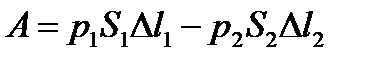где путь, который проходит столб жидкости массой m за время D t 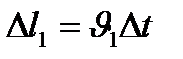в сечении S₁, а в сечении S₂ путь 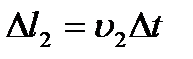. Следовательно, работа А, совершаемая потоком жидкости, равна

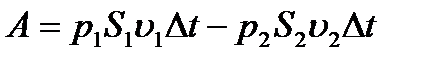
Полная энергия потока жидкости, протекающего за время D t через входное сечение S ₁, будет равна

,

а через сечение S ₂

.

Изменение полной энергии жидкости равно работе, совершенной внешними силами, т.е.

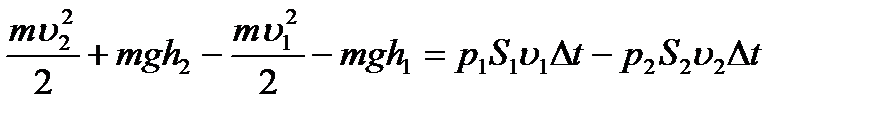(4.1)

Согласно уравнению непрерывности струи, объемы, входящие в S ₁ за время D t и выходящие через S ₂, одинаковы, поэтому можно записать

.

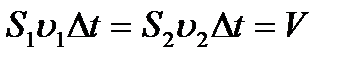Разделив левую и правую части уравнения (4.1) на объем V и используя формулу плотности 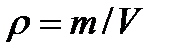, получаем для двух различных сечений трубки тока:

,

т.е. для каждого сечения трубки тока справедливо выражение:

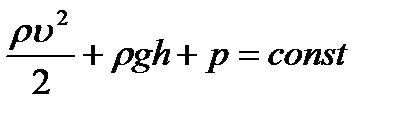, (4.2)

выражение (4.2) называется уравнением Бернулли. Слагаемое р называется статическим давлением, – гидростатическим давлением, а –называется динамическим давлением.

В качестве следствий из уравнения Бернулли рассмотрим два случая: горизонтальное течение жидкости и истечение жидкости из отверстия.

1.При горизонтальном течении жидкости все части трубки тока лежат на одном уровне, значит h =const, поэтому в уравнении (4.2) выражение можно перенести в правую сторону и объеденить с константой, и тогда

,

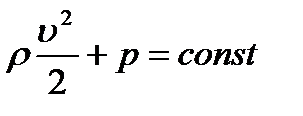т.е. при горизонтальном течении жидкости сумма динамического и статического давлений не изменяется при отсутствии трения или статическое давление невязкой жидкости при течении по горизонтальной трубке увеличивается там, где уменьшается скорость ее течения и, наоборот. Рассмотрим горизонтально расположенную трубку с переменным сечением (см. рис.4.5). Из уравнения непрерывности следует, что в суженном участке трубки будет самая большая скорость, поэтому давление статическое на этом участке будет самым маленьким, можно добиться того, что оно будет меньше атмосферного давления и тогда струя протекающей по трубке жидкости может оказывать всасывающее действие (водоструйный насос, ингаляторы).

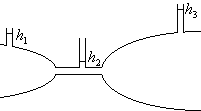Рисунок 4.5

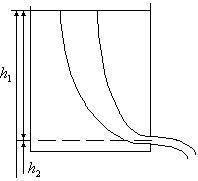Рисунок 4.6

2.Применим уравнение Бернулли (4.2) к случаю истечения жидкости из небольшого отверстия в широком открытом сосуде (см. рис.4.6) При этом будем считать, что внешнее давление (например, атмосферное) неизменно. Выделим в жидкости трубку тока, имеющую своим сечением с одной стороны открытую поверхность жидкости в сосуде, а с другой стороны – отверстие, через которое вытекает жидкость.

В сечении, расположенном на поверхности жидкости скорость одинакова по всему сечению и равна 0. В сечении, через которое жидкость вытекает, ее скорость везде одинакова и равна u. Далее давления в обоих сечениях равны атмосферному давлению и поэтому одинаковы. Применительно к данному случаю уравнение (4.2) можно записать в следующем виде

,

Сокращая на r и введя 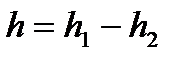– высоту открытой поверхности жидкости над отверстием, получаем:

откуда

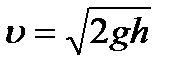, (4.3)

выражение (4.3) называется формулой Торричелли.

Итак, скорость истечения жидкости из отверстия, расположенного на глубине h под открытой поверхностью, совпадает со скоростью, которую приобретает любое тело, падая с высоты h. Следует помнить, что этот результат получен в предположении, что жидкость идеальна. Для реальных жидкостей скорость истечения меньше, причем тем сильнее отличается, чем больше вязкость жидкости. Формула (4.3) справедлива как для боковых, так и для донных отверстий и не зависит от угла наклона выходного отверстия.

Формула Торричелли, например, позволяет правильно оценить высоту расположения сосуда с лекарственным препаратом при его введении в вену.

4.3.3 Поверхностное натяжение

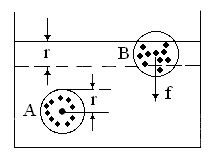Рисунок 4.7

Силы взаимодействия молекул быстро убывают с расстоянием. Поэтому можно считать, что каждая молекула взаимодействует только с теми, которые лежат внутри сферы радиуса r- сферы молекулярного действия, с центром в данной молекуле (см. рис.4.7).

Если некоторая молекула А находится глубоко внутри жидкости, то силы, действующие на нее со стороны других молекул, взаимно компенсируются. Иначе обстоит дело с молекулами находящимися у поверхности жидкости. Концентрация молекул в паре над жидкостью гораздо меньше, чем в жидкости. Поэтому на молекулу В, лежащую в верхнем слое жидкости, действует некоторая сила притяжения f, направленная внутрь жидкости. Таким образом, на каждую молекулу, лежащую на расстоянии, меньше r, от поверхности жидкости, со стороны других молекул действует сила, направленная внутрь жидкости. Следовательно, весь поверхностный слой находится в особом состоянии: он оказывает на жидкость давление, подобное давлению упругой пленки. В соответствии с этим молекулы поверхностного слоя обладают дополнительной потенциальной энергией.

Перемещение молекулы из поверхностного слоя вглубь жидкости сопровождается совершением работы, причем потенциальная энергия, которой обладала молекула в поверхностном слое, переходит в кинетическую энергию молекулы. Наоборот, переход молекулы из глубины жидкости в поверхностный слой требует затраты работы на преодоление силы f (cм. рис.4.7). Работа совершается молекулой за счет изменения ее кинетической энергии. Потенциальная энергия молекулы, попавшей в поверхностный слой, увеличивается.

В жидкости при заданных внешних условиях устанавливается равновесие, при котором число молекул в поверхностном слое с течением времени не меняется. Если же по тем или иным причинам поверхность жидкости увеличивается, то некоторое число молекул перейдет из глубины жидкости в поверхностный слой. Для этого нужно затратить внешнюю работу dA, которая пропорциональна увеличению площади поверхности dS, т.е.

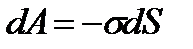
знак минус показывает, что увеличение поверхности происходит только при совершении работы внешними силами.

Коэффициент s, характеризующий свойства поверхности жидкости, называется коэффициентом поверхностного натяжения. Он измеряется работой, необходимой для увеличения поверхности жидкости при постоянной температуре на единицу площади. В системе СИ коэффициент поверхностного натяжения имеет размерность [Дж/м²].

Работа, затраченная на увеличение площади поверхности жидкости, приводит к увеличению потенциальной энергии поверхности жидкости, т.е. потенциальная энергия пропорциональна площади S поверхностного слоя. Всякая система стремиться к состоянию с минимальной энергией. Поэтому в свободном состоянии, жидкость стремиться к тому, чтобы ее поверхность была минимальна (капельки свободной жидкости всегда имеют форму сферы).

Молекулы поверхностного слоя находятся в среднем на больших расстояниях друг от друга, чем молекулы внутри жидкости. Жидкость в поверхностном слое всегда находится в растянутом, напряженном состоянии, и поэтому на границу свободной поверхности жидкости действует сила поверхностного натяжения жидкости, направленная касательно к поверхности жидкости и нормально к свободной поверхности:

,

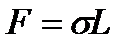где L – длина контура, ограничивающего поверхность жидкости. Коэффициент поверхностного натяжения определяется и через силу поверхностного натяжения. Второе определение коэффициента поверхностного натяжения: коэффициент поверхностного натяжения численно равен силе поверхностного натяжения, действующей на единицу длины контура, ограничивающего поверхность жидкости.

С ростом температуры взаимодействие молекул жидкости несколько ослабляется, так как при увеличении кинетической энергии молекул жидкость «разрыхляется» и среднее расстояние между молекулами возрастает. Поэтому с увеличением температуры величина коэффициента поверхностного натяжения s должна уменьшаться.

4.3.4 Смачивание и несмачивание

При рассмотрении молекулярной картины поверхностного слоя жидкости мы отмечали, что молекулы жидкости, расположенные на поверхности, разделяющей жидкость и газ (воздух или пар этой жидкости), почти не притягиваются молекулами газа (концентрация молекул газа слишком мала). Если же среда, с которой граничит рассматриваемая жидкость, достаточно плотная, то пренебрегать взаимодействием ее молекул с молекулами жидкости нельзя. Из-за этого коэффициенты поверхностного натяжения данной жидкости, граничащей с различными средами, могут значительно различаться между собой. Например, при комнатной температуре коэффициент поверхностного натяжения воды на границе вода-бензол s =0,033, а на границе вода-эфир s =0,012, на границе воды с собственным паром s =0,073 Н/м.

Поверхностное натяжение на границе различных сред играет важную роль в разнообразных поверхностных явлениях. Рассмотрим поверхностные явления, возникающие при соприкосновении жидкости с твердым телом. Если жидкость находится в сосуде, то, кроме свободной поверхности, существует еще граница раздела между жидкостью и твердым телом – стенками сосуда. Молекулы жидкости, соприкасающиеся со стенкой сосуда, взаимодействуют со своими ближайшими соседями, как жидкости, так и твердого тела. Если сила взаимодействия молекулы жидкости с молекулой жидкости больше силы взаимодействия молекулы жидкости с молекулой твердого тела, то результирующая сила направлена вглубь жидкости (см. рис.4.8).

Рисунок 4.8

Такую жидкость называют несмачивающей. Свободная поверхность жидкости у краев стенки сосуда будет выпуклой. Если сила взаимодействия молекулы жидкости с молекулой жидкости меньше силы взаимодействия молекулы жидкости с молекулой твердого тела, то результирующая сила, действующая на молекулу жидкости, находящуюся у стенки твердого тела, направлена вглубь твердого тела, т.е. молекула жидкости как бы прилипает к твердому телу. Такие жидкости называют смачивающими (см. рис.4.9). Свободная поверхность жидкости у краев стенки сосуда будет вогнутой.

Рисунок 4.9

Количественной оценкой смачивания служит краевой угол. Краевым углом называется угол Q, составленный стенкой сосуда и касательной к поверхности жидкости, проведенной из точки пересечения поверхности жидкости со стенкой сосуда. Угол отсчитывается всегда вовнутрь жидкости (см. рис.4.10). При смачивании твердого тела жидкостью краевой угол лежит в пределах: 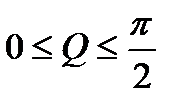. Полное смачивание бывает, тогда, когда краевой угол равен нулю .

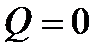Рисунок 4.10

Если жидкость является несмачивающей, то краевой угол лежит в пределах 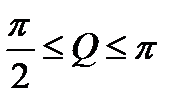. Полное несмачивание бывает в том случае, когда краевой угол равен p.

4.3.5 Зависимость молекулярного давления от кривизны

поверхности жидкости

Взаимодействие частиц жидкости с частицами твердого тела влияет на форму поверхности жидкости, налитой в сосуд. У самых стенок сосуда поверхность жидкости искривлена (см.рис.4.8, 4.9). В узких трубках (капиллярах) или в узком зазоре между двумя стенками искривлена вся поверхность жидкости. Если жидкость смачивает стенки, поверхность имеет вогнутую форму (см.рис.4.11а), если не смачивает, то выпуклую (рис.4.11б). Изогнутые поверхности жидкости в сосудах называются менисками. Благодаря действию сил поверхностного натяжения давление внутри жидкости будет отличаться на некоторую величину D p от внешнего давления газа или пара над поверхностью жидкости.

Рисунок 4.11

Оценим величину дополнительного давления в случае сферического поверхностного слоя. Выделим на поверхности сферы малый сферический сегмент. Силы поверхностного натяжения, приложенные к контуру этого сегмента, направлены по касательной к сферической поверхности (см.рис.4.12). К элементу контура D l, изображенному жирной дугой, приложена сила D f, равная по абсолютной величине .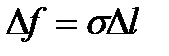

Найдем составляющую D f ₁ этой силы, параллельную радиусу кривизны ОС. Из рисунка имеем .

Именно эта составляющая и создает добавочное давление. Мы нашли составляющую силы поверхностного натяжения, действующую на элемент контура D l. Полная сила, приложенная к контуру и создающая добавочное давление, очевидно, равна

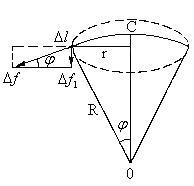Рисунок 4.12

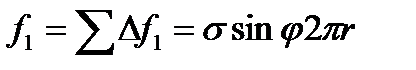
Из чертежа следует, что 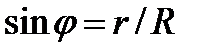, и, значит,

.

Добавочное давление D p получим, разделив силу

f ₁ на площадь сегмента 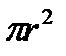, итак,

. (4.4)

Соотношение (4.4) дает величину добавочного давления под сферической поверхностью и носит название формулы Лапласа. В случае вогнутой поверхности жидкости, результирующая сила поверхностного натяжения направлена из жидкости в газ (пар). В этом случае 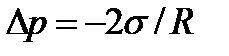, т.е. давление внутри жидкости под вогнутой поверхностью меньше, чем в газе над поверхностью жидкости на величину D р.

В общем случае произвольной поверхности двоякой кривизны формула Лапласа может быть обобщена:

.

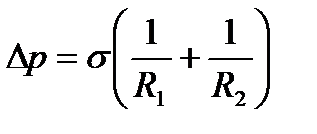В зависимости от значений и знаков радиусов кривизны R ₁ и R ₂ величина дополнительного давления D р может оказаться положительной и отрицательной.

4.3.6 Капиллярные явления

В узких трубках (капиллярах) вследствие смачивания или несмачивания жидкостью стенок капилляра кривизна поверхности жидкости (т.е. мениск) становится значительной. Возникающее при этом дополнительное давление Dр вызывает заметное поднятие или опускание уровня жидкости.

Рассмотрим для примера случай круглого капилляра радиуса r, погруженного в большой сосуд с жидкостью, не смачивающей стенки капилляра. При этом внутри капилляра образуется мениск, и под действием дополнительного давления D р жидкость в капилляре опускается на некоторую глубину, как показано на рисунке 4.13. В широком сосуде благодаря действию силы тяжести можно считать поверхность жидкости практически плоской. В узкой трубке, напротив, можно пренебречь действием сил тяжести по сравнению с силами поверхностного натяжения и поверхность жидкости можно считать сферой радиуса R. Из рисунка 4.13 видно, что

,

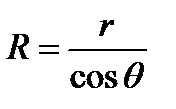где q – краевой угол на границе жидкость – твердая стенка.

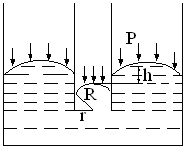Рисунок 4.13

На уровне поверхности жидкости в капилляре давление в жидкости равно

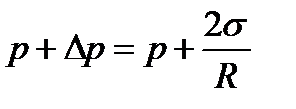, где р – внешнее давление в газе. По закону сообщающихся сосудов оно должно быть равно полному давлению на том же уровне в широком сосу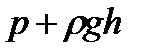де , где – гидростатическое давление столба жидкости плотности r на глубине h. Приравнивая, получим:

,

откуда

.

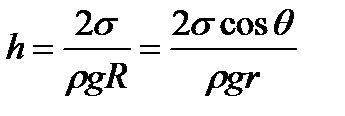Точно такое же выражение получится и для высоты поднятия жидкости, смачивающей стенки капилляра радиуса r. При полном смачивании (например, вода-стекло) 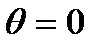, радиус мениска равен радиуса капилляра и высота поднятия жидкости равна

.

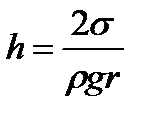Капиллярные явления играют большую роль в медицине. Чтобы жидкость не только втягивалась в капилляр, а вообще проникала в поры, необходим малый краевой угол. При большой величине краевого угла предметы будут оставаться сухими. Ниже приведены примеры, которые демонстрируют роль капиллярности и смачивания.

1. Системы, где нужен малый краевой угол (желательно при большом поверхностном натяжении): кровь на бинтах (гигроскопичность ваты), капли от насморка на слизистой оболочке носа, слюна на пище. Растворитель для краски на сухом порошке красителя, жидкая краска на окрашиваемых поверхностях (различные цвета таблеток) и т.д.

2. Системы, где нужен большой краевой угол: вода на стеклах очков (мелкие капли быстрей испаряются), защитные кремы и т.д.

4.3.7 Поверхностно-активные вещества

Многие вещества понижают поверхностное натяжение жидкостей. Такие вещества называются поверхностно-активными (мыло, масляная кислота).

Для достижения минимума поверхностной энергии поверхностно-активное вещество должно концентрироваться у поверхности жидкости или твердого тела. Увеличение концентрации растворенных веществ, понижающих поверхностное натяжение у поверхности жидкости или твердых тел, называется адсорбцией. Она может происходить не только на свободной поверхности жидкости, но и на поверхности соприкосновения двух жидкостей или на поверхности раздела жидкости и твердого тела. Для адсорбции необходимо только, чтобы растворенное вещество понижало поверхностное натяжение на данной поверхности. Тела, на поверхности которых концентрируются поверхностно-активные вещества, называются адсорбентами.

Простейшими поверхностно-активными веществами по отношению к воде являются спирты, жирные кислоты и их соли.

4.3.8 Явления переноса

Если молекулы жидкости или газа отличаются одна от другой какой-либо характерной величиной (массой, импульсом, энергией и др.), причем распределение молекул по значениям указанной характеристики неоднородно, то вследствие теплового движения эта величина «переносится» из одного места в другое. В результате возникает поток рассматриваемой величины (массы, импульса, энергии), обуславливающей ряд явлений, называемых явлениями переноса.

Вязкость (внутреннее трение). Рассмотрим поток жидкости или газа, в котором скорость течения жидкости во всех точках одинакова по направлению, но меняется по величине вдоль перпендикуляра к скорости 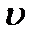. Мы выберем направление этого перпендикуляра вдоль оси x (см. рис.4.14); тогда скорость является функцией от координаты х: . Можно сказать, что поток разделяется на параллельные между собой слои, движущиеся с различной скоростью, но параллельно друг другу.

Рисунок 4.14

Вследствие теплового движения молекулы переходят из одного слоя в другой, перенося с собой импульс (m 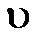) своего направленного движения. В результате возникает процесс переноса импульса из тех слоев, где скорость потока больше, в те слои, где она меньше и наоборот. За счет переноса импульса от быстрых слоев к медленным слоям и наоборот, происходит изменение импульса слоев (быстрые слои замедляются, медленные ускоряются). Второй закон Ньютона утверждает, что изменение импульса может происходить, только под действием импульса силы: 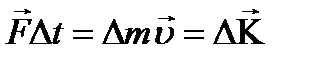. Значит, между слоями существуют силы и называются они силами внутреннего трения. А процесс, приводящий к выравниванию скоростей течения различных слоев, называется внутренним трением или вязкостью.

Основное уравнение, описывающее силу внутреннего трения, выглядит следующим образом:

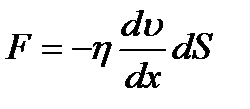
И носит название уравнения Ньютона. В уравнение входит коэффициент h, который называется коэффициентом вязкости. Из уравнения Ньютона следует, что коэффициент вязкости равен:

,

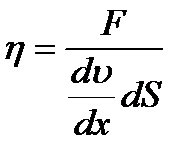т.е. коэффициент вязкости это физическая величина, численно равная силе, действующей между слоями жидкости, площадь соприкосновения которых равна 1 и градиент скоростей, между которыми также равен 1. Величина 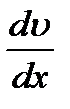называется градиентом скоростей. Градиент скоростей показывает изменение скорости течения жидкости в направлении перпендикулярном направлению течения жидкости.

Вязкость жидкости обычно во много раз больше, чем вязкость газа. С ростом температуры вязкость жидкости быстро падает, а вязкость газа медленно возрастает.

Для многих жидкостей вязкость зависит только от температуры и давления. Эти жидкости называются ньютоновскими.

Неньютоновскими жидкостями являются жидкости, у которых при постоянной температуре и давлении вязкость зависит от градиента скорости и других факторов. К неньютоновским жидкостям относятся кровь, высокодисперсные суспензии.

Вязкость жидкости определяет силу сопротивления жидкости движению в ней тел. Таким образом, сила сопротивления движению шарика радиуса r при малых скоростях движения находится по уравнению Стокса

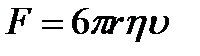
эта сила прямо пропорциональна вязкости среды h и скорости движения шарика u. Замеряя скорость шарика, можно найти вязкость среды.

Перенос молекул вещества за счет теплового движения из области, где концентрация вещества больше в область с меньшей концентрацией называется диффузией. В результате диффузии происходит выравнивание концентраций. Масса вещества, диффундировавшего через площадку D S за время D t, определяется законом Фика:

,

где С – концентрация диффундирующих молекул, 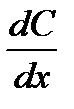– градиент этой концентрации, D – коэффициент диффузии, который зависит от свойств диффундирующего вещества и условий, в которых оно находится.

Обратим внимание, что чем выше температура жидкости, тем меньшее число колебаний совершает молекула в положении равновесия до своего перескока, тем интенсивнее процесс диффузии и тем выше величина D. Однако коэффициенты диффузии в жидкости все же имеют порядок 10^-5см²/с, что во много раз меньше, чем в газах.

Явление теплопроводности заключается в том, что молекулы от более горячего слоя с температурой T ₁, где они имеют большую кинетическую энергию, проникают в более холодный слой с температурой T ₂ и переносят при этом свою кинетическую энергию, что создает поток тепла Q. Закон теплопроводности установлен Фурье:

,

где c – коэффициент теплопроводности, – градиент температур. Коэффициент теплопроводности не зависит от давления, но зависит от температуры, приближенно можно считать, что .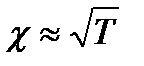

4.3.9 Ламинарное и турбулентное течение жидкости

Мы уже обсуждали, что наблюдается два течения жидкости или газа: ламинарное течение жидкости и турбулентное. Обычно ламинарное течение жидкости устанавливается в трубках с гладкими стенками без резких изменений площади сечений и резких изгибов трубки. При нарушении этих условий, а особенно при высоких скоростях, течение жидкости переходит в турбулентное, т.е. вихревое (см. рис. 4.1). Скорость течения жидкости будет разной в разных точках спирали, значит, будут наблюдаться местные изменения давления в жидкости, вызывающие колебательные движения частиц, сопровождающиеся звуковыми явлениями (шум, журчание), благодаря этому турбулентное течение легко обнаруживается.

Английский ученый Рейнольдс установил, характер течения зависит от значения безразмерной величины:

, (4.5)

где r – плотность жидкости или газа, – средняя по сечению трубы скорость потока, h – коэффициент вязкости жидкости, D – характерный для поперечного сечения размер, например, сторона квадрата при квадратном сечении, радиус при круглом сечении.

Величина Re называется числом Рейнольдса. При малых значениях числа Рейнольдса наблюдается ламинарное течение жидкости. Начиная с некоторого определенного значения Re, называемого критическим, течение приобретает турбулентный характер. Если в качестве характерного размера для круглой трубы взять ее диаметр, то критическое значение числа Рейнольдса оказывается примерно 2000. Характер течения различных жидкостей или газов в трубах разных сечений будет совершенно одинаков, если каждому течению соответствует одно и то же значение числа Рейнольдса.

4.3.10 Формула Пуазейля

Объем жидкости, протекающей через поперечное сечение круглой трубы в единицу времени при ламинарном течении зависит от вязкости жидкости, разности давлений и размеров трубки, по которой течет жидкость. Обозначим dQ – объемную скорость жидкости, эта скорость равна объему жидкости, протекающему через поперечное сечение трубки в единицу времени:

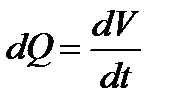. (4.6)

Найдем связь между линейной и объемной скоростями жидкости. Выделим в трубке небольшой объем в форме цилиндра, площадь поперечного сечения этого цилиндра равна d S, а длина равна d l, тогда объем этого цилиндра 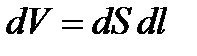. Длину цилиндра можно выразить через линейную скорость течения жидкости следующим образом 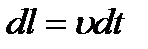, тогда . Подставим это выражение в уравнение (4.6), получим:

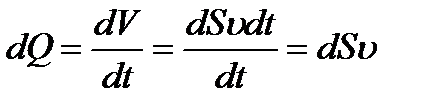. (4.7)

Таким образом, объемная скорость течения жидкости по сосуду равна линейной скоростью течения жидкости умноженной на площадь поперечного сечения.

Течение вязкой жидкости по трубам представляет для медицины особый интерес, так как кровеносная система состоит в основном из цилиндрических сосудов разного диаметра. Французский врач Жан Луи Мари Пуазейль работал по вопросам кровообращения и дыхания, поэтому заинтересовался вопросами гидродинамики. Им была получена формула, которая получила название формулы Пуазейля, которая устанавливает связь между объемной скоростью течения жидкости, вязкостью жидкости и разностью давлений на концах цилиндрической трубки при ламинарном течении жидкости:

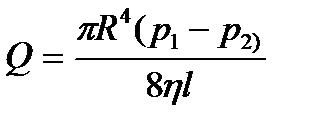, (4.8)

где R – внутренний радиус трубки, по которой течет жидкость, – разность давлений на концах трубки, h – вязкость жидкости, текущей по трубке.

Если бы жидкость не обладала вязкостью, то для течения по горизонтальной трубе не требовалось бы прилагать ни какую силу, но благодаря вязкости стационарное течение любой реальной жидкости в трубе возможно лишь тогда, когда между концами трубы создана разность давлений – будь это вода в водопроводной воде или кровь в кровеносной системе.

Согласно формуле Пуазейля, поток жидкости Q пропорционален градиенту давления и обратно пропорционален вязкости жидкости (газа), чего и следовало ожидать. Однако может показаться удивительным, что Q зависит от четвертой степени радиуса трубы. Это означает, что при одном и том же градиенте давления увеличение радиуса трубы вдвое приведет к увеличению потока в шестнадцать раз! Таким образом, даже небольшое изменение радиуса трубы приводит к значительному изменению потока жидкости; для того же, чтобы поддерживать поток на прежнем уровне, пришлось бы заметно изменить разность давлений.

Интересный пример зависимости вида R ⁴можно найти в системе кровообращения человеческого организма. Однако, поскольку формула Пуазейля справедлива лишь для ламинарного течения несжимаемой жидкости с постоянной вязкостью h, она не может в точности выполняться для крови; дело в том, что течение крови не вполне ламинарно, кровь содержит взвешенные частицы, диаметр которых почти равен диаметру капилляров, а ее вязкость h зависит от скорости течения . Тем не менее, и в этом случае формула Пуазейля является хорошим приближением в первом порядке. Поток крови в организме регулируется крошечными мышцами, окружающими сосуды. При сокращении этих мышц диаметр сосуда уменьшается и поток, который в соответствии с формулой Пуазейля пропорционален R ⁴, резко уменьшается уже при небольшом уменьшении радиуса. Таким образом, едва заметными сокращениями этих мышц очень точно контролируется поступление крови к различным органам. Однако если, скажем, вследствие атеросклероза (затвердевания стенок сосудов) и отложений холестерина радиус сосудов уменьшается, то для поддержания нормального кровотока требуется более высокий градиент давления. Если радиус сосудов уменьшится вдвое, то сердцу придется увеличить давление в 16 раз. В таких условиях сердце работает с перегрузкой, но, как правило, уже не может обеспечить требуемую величину потока жидкости, т.е. нормальное кровообращение.

Таким образом, повышенное артериальное давление указывает и на то, что сердце работает с перегрузкой, и на то, что поток крови через артерии ниже нормы.

Поиск по сайту: