Виды механического движения материальной точки

1) Равномерное прямолинейное движение. Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. При этом вектор скорости не меняется ни по величине, ни по направлению, модуль вектора перемещения равен пройденному телом пути, мгновенная и средняя скорости совпадают. Это движение описывается уравнением движения

или .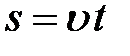

2) Равнопеременное, прямолинейное движение. Равнопеременным, прямолинейным движением называется движение, при котором тангенциальное ускорение является постоянной величиной. Оно не меняется ни по величине, ни по направлению (). При таком движении нормальное ускорение равно нулю . В этом случае полное ускорение равно тангенциальному и равно , а скорость в любой момент времени движения материальной точки находится следующим образом . Путь, пройденный материальной точкой при данном движении, находится следующим образом:

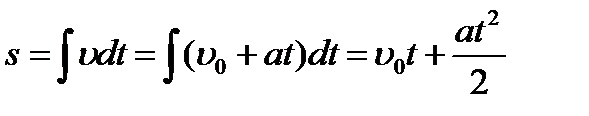
или в координатном виде

.

Рисунок 1.4

3) Равномерное движение по окружности. Равномерным движением по окружности называется движение, при котором тангенциальное ускорение равно нулю 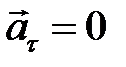, а нормальное ускорение меняется по направлению, но не меняется по величине , в этом случае траекторией материальной точки будет окружность. Описать движение материальной точки по окружности можно и с помощью линейных характеристик (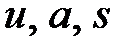) и с помощью угловых характеристик: углового пути , угловой скорости . Рассмотрим связь между линейными и угловыми характеристиками движения материальной точки. Перемещаясь из точки 1 в точку 2 (см. рисунок 1.4), материальная точка проходит путь 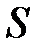, равный длине дуги окружности радиуса и поворачивается на угол , который и равен угловому пути, пройденному материальной точкой. Угол j – это центральный угол, поэтому . Используя эту связь между пройденным линейным и угловым расстоянием, получим

.

Таким образом, линейная скорость связана с угловой скоростью следующим образом:

.

Поскольку равномерное движение по окружности характеризуется постоянным по величине нормальным ускорением, то выразим его модуль через угловые характеристики:

Таким образом, модуль нормального ускорения равен .

Рисунок 1.5 Изменение скорости частицы, движущейся по окружности.

Вместо V вставить u

Заметьте, что в любой момент времени мгновенная скорость направлена по касательной к круговой траектории.

Рисунок 1.6

При равномерном вращательном движении вектор ускорения всегда перпендикулярен вектору скорости .

Вместо V вставить u

4) Ускоренное движение по окружности

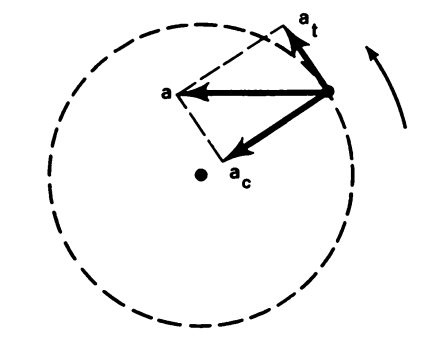
Рисунок 1.7

При неравномерном вращательном движении ускорение имеет как тангенциальную (), так и центростремительную () составляющие. В этом случае меняется по величине линейная скорость, а, следовательно, и угловая скорость (см. рисунок 1.7). Изменение угловой скорости характеризуется угловым ускорением. Угловым ускорением называется изменение угловой скорости в единицу времени:

.

Если угловое ускорение является постоянным, то движение по окружности называется равнопеременным. Аналогично прямолинейному равнопеременному движению, равнопеременное движение по окружности можно описать следующими уравнениями движения:

,

,

где – это начальная угловая скорость движения материальной точки. Достаточно часто требуется выразить угловой путь через число оборотов. При этом следует помнить, что за один оборот материальная точка проходит угловой путь равный 2 p, поэтому если материальная точка совершила оборотов, то, значит, она прошла угловой путь равный , .

Рисунок 1.8

В технике вращательное движение встречается чрезвычайно часто: вращение валов двигателей и генераторов, колес, турбин и пропеллеров самолетов, центрифуг и т.д. В живых организмах устройства подобных вращающемуся колесу, можно встретить у многих бактерий, например, у кишечной палочки, имеется «мотор», вращающий жгутики. С помощью этих жгутиков бактерия перемещается в среде (см. рисунок 1.8 а). Основание жгутика прикреплено к колесику (ротору) в форме кольца (см. рисунок 1.8 б). Плоскость ротора параллельна другому кольцу, закрепленному в мембране клетки. Ротор вращается, делая до восьми оборотов в секунду.

Проверьте себя

1) По какой траектории движется материальная точка, если

а) радиус-вектор изменяется только по величине?

б) радиус-вектор изменяется только по направлению?

в) радиус-вектор изменяется как по направлению, так и по величине?

2) Сформулируйте понятия:

а) материальной точки

б) траектории

в) пути и перемещения

г) мгновенной скорости.

3) Чем отличается путь от перемещения?

4) Как направлена мгновенная скорость?

5) Как находится нормальное ускорение и как оно направлено?

6) Как найти тангенциальное ускорение, и как оно направлено?

7) Покажите, что полное ускорение равно геометрической сумме тангенциального и нормального ускорений.

8) Может ли тело в один и тот же момент времени иметь равную нулю скорость и не равное нулю ускорение?

9) Чем отличается равномерное движение по окружности от прямолинейного равномерного движения?

10) Дайте понятия угловой скорости и углового ускорения.

11) Запишите уравнение движения для равнопеременного движения по окружности.

12) Как связаны между собой линейные и угловые характеристики движения материальной точки по окружности?

Поиск по сайту: