Вопрос 26 : Свободные гармонические механические колебания и их характеристики. Математический и физический маятники

Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид x Характеристики: 1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени. 2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.

3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [ T ] = 1 с. 4) Частота колебаний ν − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [ ν ]= 1 Гц. Частота определяется по формуле 5) Циклическая частота ω − это величина, равная числу полных колебаний, совершающихся за 2π секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2 π циклов колебаний, [ ω]= с^-1. Циклическая частота связана с периодом и частотой колебаний соотношением

6)Фаза колебаний ωt+φ0 – фаза указывает местоположение колеблющейся точки в данный момент времени. 7) Начальная фаза φ0 − указывает местоположение колеблющейся точки в момент времени t=0.

1) Математический маятник − это идеализированная система состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m. Отклонение маятника от положения равновесия будем характеризовать углом φ, образованным нитью с вертикалью. При отклонении маятника от положения равновесия возникает вращательный момент M, равный по величине mglsinφ. Он имеет такое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для вращательного момента имеет вид: M=mglsinφ. Применим основное уравнение динамики вращательного движения M=Iε, где I=ml² – момент инерции материальной точки. Тогда, учитывая, что угловое ускорение , получим

Если рассматривать малые колебания, то sinφ ≈φ. Получим То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой Период колебаний математического маятника

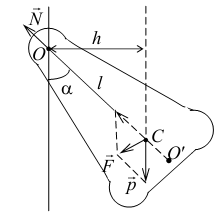
2) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен . Согласно основному уравнению динамики вращательного движения получаем

где I − момент инерции маятника относительно оси, проходящей через точку подвеса. Если рассматривать малые колебания, то sinφ≈φ. Получим

То есть при малых колебаниях угловое отклонение физического маятника изменяется по гармоническому закону с частотой

Период колебаний физического маятника

Поиск по сайту: