 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Резонанс механических колебаний
Резонанс - явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой к собственной частоте колебательной системы.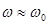 
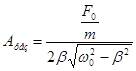
При резонансной частоте амплитуда вынужденных колебаний имеет максимум. Чем меньше β, тем больше 
. В случае β=0, 
и 
, что физически бессмысленно.
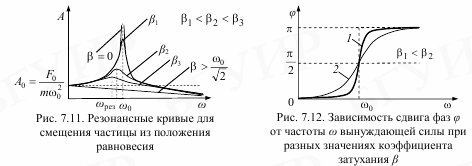
В реальных условиях на осциллятор всегда действуют силы сопротивления среды. При слабом затухании 
и значение ϕ при резонансе практически равно 
. Если β становится настолько большим, что 
, то выражение для резонансной частоты становится мнимым. Следовательно, резонанс отсутствует, амплитуда монотонно уменьшается с увеличением частоты вынуждающей силы.
При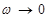 
амплитуда достигает статистического отклонения 
- предельного значения смещения под действием постоянной силы 
(случай статистической деформации системы под действием постоянной силы , когда 
).
При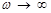 
амплитуда стремится к 0. При большой частоте система не успевает колебаться и смещения относительно положения равновесия нет.
В случае малого затухания (
) внешняя сила компенсирует в точке резонанса силу сопротивления среды, резонансная амплитуда
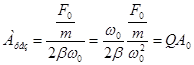,где 
-добротность колебательной системы; 
- статистическое отклонение. Следовательно, чем больше , тем больше 
.
Поиск по сайту: