АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение уравнения Шредингера для свободной частицы

Читайте также:
  1. I. Решение логических задач средствами алгебры логики
  2. II. Решение логических задач табличным способом
  3. III. Разрешение споров в международных организациях.
  4. III. Решение логических задач с помощью рассуждений
  5. Алгебраические уравнения
  6. Антиполия-противоречие в в законе. Противоречие разрешаясь делает чего то возможным. Отрицание-отрицания ( разрешение противоречия (синтез))
  7. Античастицы. Аннигиляция.
  8. Б) Правовое разрешение конфликтов
  9. В результате получаем общее решение системы
  10. Волна вероятности. Уравнение Шредингера
  11. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  12. Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.

Рассмотрим волновую функцию свободной микрочастицы, которая имеет определенные значения импульса р и энергии Е, т. е. движется со скоростью υ, например, вдоль оси Ох (ру = рz = 0). Так как из опытов следует, что параллельный пучок элементарных частиц обладает свойствами плоской волны распространяющейся в направлении скорости частиц, то рассмотрим в общем виде плоскую волну распространяющуюся вдоль Ох. Запишем волновую функцию свободной частицы в комплексном виде по аналогии с уравнением плоской волны.

Ψ= 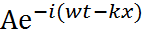=Acos(wt-kx) – isin(wt-kx) (8.6.1)

Преобразуем выражение (8.6.1), используя формулы взаимосвязи импульса р и энергии Е частицы (корпускулярных характеристик) с волновым числом k и циклической частотой ω (с волновыми характеристиками частицы)

 

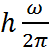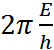E= = ⇒ ω= = (8.6.2)

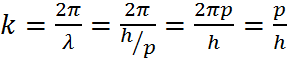(8.6.3)

Подставим (8.6.2−8.6.3) в уравнение (8.6.1) и получим

(8.6.5)

Применим к ψ оператор Лапласа и получим уравнение Шредингера для свободной частицы

Δψ+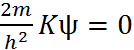


 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)