АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Закон изменения и сохранения момента импульса МТ и АТТ. Скамья Жуковского

Читайте также:
  1. B) Наличное бытие закона
  2. II закон Кирхгофа
  3. II. Законодательные акты Украины
  4. II. Законодательство об охране труда
  5. II.3. Закон как категория публичного права
  6. III. Государственный надзор и контроль за соблюдением законодательства об охране труда
  7. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  8. IX.3.Закономерности развития науки.
  9. А 55. ЗАКОНОМІРНОСТІ ДІЇ КОЛОГИЧЕСКИХ ФАКТОРІВ НА ЖИВІ ОРГАНІЗМИ
  10. А) Закон диалектического синтеза
  11. А) совокупность предусмотренных законодательством видов и ставок налога, принципов, форм и методов их установления.
  12. А. Законодательные (представительные) органы власти республик в составе Российской Федерации

Моментом импульса материальной точки А называется относительно неподвижной точки О называется физическая величина, определяемая величина, определяемая произведением: , где r- радиус-вектор, проведённый из точки О в точку А, р-импульс МТ

Модуль , 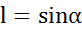-плечо ветора р, длина перпендикуляра из точки О на прямую вдоль направления р.

перпенд.r и перпенд. р. [L]=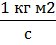

Момент импульса АТТ вокруг неподвижной оси z: . -уравнение динамики вращетельного движения АТТ.

Момент силы отн. точки О-векторное произведение Модуль М(модуль моментасилы): M=rFsinα=lF [M]=1Hм, l-плечо силы. Сумма моментов всех внешних сил: . М характеризует способность силы вращать вокруг оси О, отн. которой определяется М.

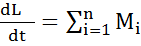– основное уравнение динамики вращательного движения системы относительно центра.

; в замкнутой системе момент внешних сил M=0, , откуда L=const-закон сохранения импульса.

Продемонстрировать закон сохранения момента импульса можно с помощью скамьи Жуковского. Пусть человек, сидящий на скамье, которая без трения вращается вокруг вертикальной оси, и держащий на вытянутых руках гантели, приведён во вращение с w1. Человек прижимает гантели-момент инерции системы уменьшается. Момент внешних сил равен 0, момент импульса системы сохраняется и w2 возрастает.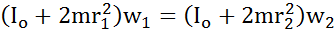



1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)