 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Квантовый гармонический осциллятор
Квант. Гарм. Осциллятор - определяется как повед. частиц m с пот. энергией U(x)= 
Потенциальная энергия такого осциллятора имеет вид
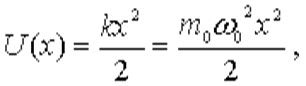
| (4.77) |
где  - собственная частота классического гармонического осциллятора. Таким образом, квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы в параболической потенциальной яме.
- собственная частота классического гармонического осциллятора. Таким образом, квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы в параболической потенциальной яме.
В квантовой механике для решения задачи о гармоническом осцилляторе нужно решить уравнение Шредингера с потенциальной энергией

| (4.78) |
Выражая, согласно, энергию осциллятора  через
через  , получаем
, получаем

49. Прохождение частицы через барьер. Туннельный эффект.
Туннельный эффект (туннелирование) – преодоление частицей потенциального барьера, когда её энергия Е меньше высоты барьера U0.
При Е > U0 есть вероятность того, что частица отразится от барьера и будет двигаться в другую сторону.
При Е < U0 частица окажется в области x > l, где l – ширина барьера.
Вероятность проникновения электрона через потенциальный барьер зависит от высоты барьера U0, его ширины l, где m – масса частицы, E – ее энергия, h – постоянная Планка (ћ = h/2π).
Коэффициент прозрачности потенциального барьера:


Молекулярная физика, макросистемы и положения МКТ. Идеальный газ. Эргодическая гипотеза. Постоянные в молекулярной физике. Основное уравнение молекулярно-кинетической теории – вывод.
Основа молекулярной физики – молекулярно-кинетическая теория. Молекулярная физика изучает свойства макроскопических систем – все тела, состоящие из огромного числа непрерывно движущихся молекул, так как с помощью только законов динамики нельзя объяснить свойства макросистем.
Методы изучения:
1) Термодинамический метод – использование опытных фактов, на их основе устанавливаются физические закономерности.
2) Статистический метод – использование теории вероятности (наука о случайных событиях # скорость молекулы, ее энергия и координаты).
Положения МКТ:
1) Идеальный газ состоит из частиц, атомов или молекул, которые находятся в непрерывном движении.
2) Размеры молекул малы, по сравнению с расстояние между ними.
3) Атомы и молекулы идеального газа взаимодействуют только за счет упругих столкновений друг с другом.
4) При отсутствии внешних сил молекулы идеального газа распределяются равномерно по всему объему.
5) Движение атомов или молекул описывается законами Классической механики.
Идеальный газ – газ, потенциальной энергией взаимодействия молекул которого можно пренебречь.
Законы идеального газа – изопроцессы – опытные законы, связывающие термодинамические параметры p, V, T газа с неизменной массой, находящегося в термодинамическом равновесии:
1) Закон Бойля – Мариотта (изотермический T = const) – pV=const
2) Закон Гей – Люссака (изобарный p = const) – V/T = const
3) Закон Шарля (изохорный V = const) – p/T = const
4) Закон Клапейрона – Менделеева – объединенный газовый закон для всех изопроцессов – 
5) Закон Авогадро – 1 моль любого ИГ при одинаковых давлении и температуре занимают одинаковый объем.
6) Закон Дальтона – давление смеси газов равно сумме парциальных давлений.
7) Нормальные условия: T = 273 K, p = 1.013*105 Па (1 атм)
Эргодическая гипотеза: в состояния термодинамического равновесия все физические величины, для описания 1 частицы идеального газа, усредняются по N частицам: 
1. Средняя арифметическая скорость 
2. Средняя квадратичная скорость 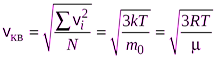
3. Наиболее вероятная скорость 
Постоянные в молекулярной физике:
1) Число Авогадро – 6,02*1023 моль-1
2) Постоянная Больцмана – K = 1.38*10-23 Дж/K
3) Универсальная газовая постоянная – R = K*Na = 8.31 Дж/К
Поиск по сайту: