Квантовый осциллятор

В классической механике:

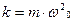, где т.к.

Перейдем теперь к квантовой механике:

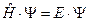(II.48)

(II.49)

Подставляя гамильтониан в стационарное уравнение Шрёдингера, получаем:

(II.50)

Разделим уравнение (II.50) на и умножим полученный результат на два:

Введем безразмерные величины:

, , (II.51)

(II.52)

Найдем конечные, непрерывные и однозначные волновые функции в интервале , удовлетворяющие уравнению (II.52). Оно имеет решение при

, где (II.53)

Это функции вида:

(II.54)

здесь - полиномы Эрмита-Чебышева n-го порядка:

(II.55)

, то есть эти волновые функции подчиняются условию нормировки. Сравнивая (II.51) и (II.53), получаем:

(II.56)

n – номер энергетического уровня Е, то есть главное квантовое число. Из (II.54) и (II.55) видно, что четность состояний определяется четностью главного квантового числа “ n ”.

Точка, в которой волновая функция равна нулю, называется узлом. То есть в такой точке вероятность обнаружить микрочастицу равна нулю. В случае квантового гармонического осциллятора число узлов равно главному квантовому числу n.

Необходимо отметить принципиальную разницу между классическим и квантовым гармоническим осциллятором.

По классической теории наименьшая энергия Е_min = 0 и соответствует покоящейся в положении равновесия частице. По квантовой теории наименьшее значение энергии осциллятора есть:

(II.57)

Она называется нулевой энергией. Выясним ее физический смысл. Среднее значение энергии осциллятора равно:

(II.58)

Соотношение неопределенностей:

(II.59)

Поскольку для осциллятора средние значения импульса и координаты равны нулю ( =0 и =0) то:

и

Отсюда можно написать в соответствии (II.59):

(II.60)

Объединив (II.58) и (II.60), получаем следующее неравенство:

(II.61)

Отсюда можно найти E_min:

Отсюда:

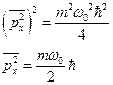и (II.62)

Подставим (II.62) в (II.61), получим следующее неравенство:

(II.63)

То есть нулевая энергия есть наименьшая энергия, совместимая с соотношением неопределенностей.

Поиск по сайту: