Энергия. Начнем с закона сохранения, связанного с однородностью времени, т.е

Начнем с закона сохранения, связанного с однородностью времени, т.е. с эквивалентностью всех моментов времени. Рассмотрим систему материальных точек, взаимодействующих друг с другом, но не взаимодействующих ни с какими посторонними телами. Такую систему называют замкнутой. Функция Лагранжа такой системы не зависит от времени явно, поэтому

(I.11)

Если бы L зависела явно от времени, был бы еще один член . Из уравнений Лагранжа для системы материальных точек следует:

(I.12)

Подставим в (I.11) вместо первого члена 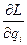выражение (I.12) и получим:

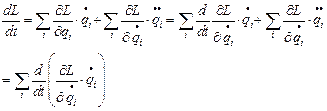
Или , т.е. величина 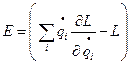неизменна во времени при движении замкнутой системы.

Эта величина называется энергией системы и является одним из ее интегралов движения.

Это будет справедливо и для систем, находящихся в постоянном внешнемполе. Механические системы, энергия которых сохраняется, называются консервативными. Теперь вспомним, что .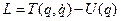

По теореме Эйлера об однородных функциях для однородной функции m-го порядка

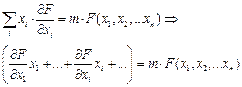
У нас T – однородная функция второго порядка (m=2)

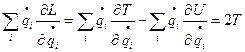
( =0, так как потенциальная энергия 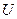не зависит от ). Следовательно, ,

или

(I.13)

В декартовых координатах оказывается, что и мы знаем, что

(I.14)

Таким образом, энергия системы может быть представлена в виде двух суммы двух ее типов: кинетической энергии, зависящей от скоростей, и потенциальной, зависящей от взаимного расположения материальных точек (или координат частиц).

Поиск по сайту: