Умножение

Пусть 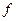и 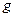– одновременно измеримые физические величины. Их произведением является величина, собственные значения которой равны произведению собственных значений величин 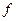и 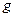. Такой величине соответствует оператор, действие которого состоит в последовательном действии на функцию сначала одного, а затем другого оператора. Такой оператор изображается математически как произведение операторов 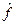и .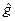

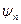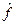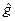Действительно, если – общие собственные функции операторов и , то

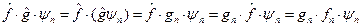(II.15)

Символ означает оператор, действие которого на функцию заключается в последовательном действии сначала оператора 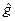на функцию , а затем уже оператора 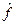на функцию .

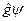Очевидно, что при названных условиях

,

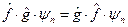так как

(II.16)

Поскольку всякая может быть представлена как 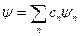, то одинаковым будет результат воздействия и 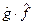на произвольную волновую функцию . Это записывается как 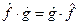или . Это коммутативные друг с другом операторы.

Таким образом, мы получили важный результат:

Если две величины 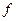и 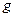имеют одновременно определенные значения, то их операторы коммутируют друг с другом или коммутативны, что одно и то же.

Физический смысл этого утверждения заключается в том, что в этом случае две данные величины могут быть измерены одновременно.

Выражение называется коммутатором. И более кратко записывается как .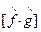

Если оно равно нулю, то эти операторы коммутируют и .

Можно показать и обратное, то есть, что если два оператора 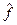и 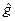коммутируют, то они имеют общую систему собственных функций.

Пример.

Найдем значение коммутатора для 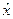и :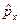

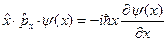
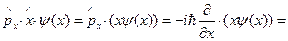
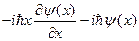
Вычтем получившиеся выражения друг из друга:

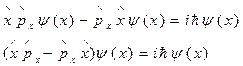(II.17)

Теперь отбросим в последнем равенстве волновую функцию 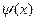и получим значение вычисляемого коммутатора .

Этот результат полностью согласуется с принципом неопределенности Гейзенберга - координата и компонента импульса в направлении этой координаты не могут быть измерены одновременно.

Поиск по сайту: