Умножение матриц

Матрица С называется произведением матрицы А на матрицу В, если ее элементы вычисляются следующим образом:

.

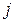Т.е. элемент матрицы С, стоящий в -той строке и -том столбце, равен сумме произведений соответствующих элементов -той строки матрицы А и 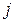-того столбца матрицы В (соответствующих — это значит, что первый элемент строки умножаем на первый элемент столбца, второй — на второй и так до последней пары элементов).

Из определения данного действия следует, что умножать можно только такие матрицы, в которых число столбцов матрицы А (т.е. число элементов в ее строке) равно числу строк матрицы В (т.е. числу элементов в ее столбце). Такие матрицы называются согласованными для умножения. Приведем примеры умножения матриц.

Пример 1. .

Пример 2.

Пример 3. .

Пример 4.

.

.

Как видно из приведенных примеров и как следует из определения произведения матриц, размер матрицы-произведения отличается от размера матриц-сомножителей. В общем случае, умножение матрицы А размера 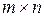на матрицу В размера дает матрицу С размера .

Произведение матриц имеет ряд особенностей по сравнению с произведением чисел. Например, не всегда возможно перемножить матрицы в обратном порядке, в примерах 3 и 4 этого сделать нельзя. Но даже если такое умножение возможно, как, например, для квадратных матриц одного порядка, могут возникнуть сюрпризы.

Пример 5.

Во-первых, произведение ненулевых матриц может дать нулевую матрицу, во-вторых, результат умножения зависит от порядка сомножителей, т.е. для произведения матриц в общем случае перестановочное свойство не выполняется. Поскольку произведение матриц в дальнейшем будет активно использоваться, укажем его свойства.

Поиск по сайту: