Вычисление собственных значений и собственных векторов матриц

Определение. Вековым определителем матрицы называется определитель вида:

.

Определение. Собственным значением квадратной матрицы А называется такое число l, для которого выполняется соотношение:

, (5.1)

если - некоторый не нулевой вектор, называемый собственным вектором матрицы А, соответствующим собственному значению l.

Соотношение (1) можно переписать в виде:

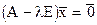, (5.2)

Условием существования ненулевого решения однородной системы (5.2) является требование:

, (5.3)

Это уравнение называется характеристическим уравнением матрицы А.

Все методы нахождения собственных значений и соответствующим им собственных векторов можно разделить на два класса: точные и итерационные.

К точным методам относятся те, что сначала строят собственный многочлен матрицы, а затем, находя его корни, получают собственные значения. По найденным собственным значениям находят соответствующие им собственные вектора, не прибегая к решению однородных систем линейных алгебраических уравнений.

К итерационным методам относятся те методы, в которых собственные значения матрицы определяются без обращения к собственному многочлену, при этом обычно одновременно вычисляются и соответствующие им собственные векторы. Вычислительные схемы таких методов носят итерационных характер.

При решении данных задач необходимо знать, что все собственные значения лежит в интервале, определяемом нормой исходной матрицы:

,

где - норма матрицы А, которая может быть посчитана двумя способами:

a) евклидова норма

b) сумма максимума модулей по строкам

Для проверки правильности решения полной проблемы собственных значений можно использовать следующие два равенства:

, .

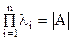Поиск по сайту: