Кусочно-линейное и кусочно-квадратичное интерполирование

Иногда, интерполирование по всей совокупности точек бывает не достаточным. В этих случаях можно воспользоваться объединением фрагментов графиков полиномов низкой степени и интерполированием между последовательными узлами. Самый простой в использовании полином первой степени. Он создает ломаную, состоящую из отрезков, которые проходят через две точки. Чтобы представить эту кусочно-линейную кривую, используется полином Лагранжа:

или используя формулу угла наклона отрезка линии в точке:

,

где 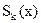- линейный сплайн на отрезке [x_k+1, x_k], y_k – заданное значение функции, полученное экспериментально в заданных узлах. Аналогично можно построить кусочно-квадратичный полином.

Недостатком этого подхода является резкое изменение кривизны в общих узлах.

Пример: Для функции y=f(x), заданной таблично осуществить кусочно-линейное интерполирование и кусочно-квадратичное интерполирование.

Решение: Осуществим кусочно-линейное интерполирование. Для этого разобьем данную функцию на элементарные промежутки, определяемые соседними числами верхней строки таблицы, и на каждом из участков строим прямую линию (полином первой степени), т.е.

Рис. 3.1. График полученного кусочно-линейного интерполирования.

Осуществим кусочно-квадратичное интерполирование. Для этого будем рассматривать тройки известных точек отрезков [0;1],[1;3],[3;5]. На каждом из этих отрезках по известным точкам построим полином второй степени. В результате получим:

Рис.3.2. График полученного кусочно-квадратичного интерполирования.

Поиск по сайту: