Вычисление всех собственных значений положительно определенной симметрической матрицы

Собственные значения такой матрицы вещественные и положительные, а собственные векторы выбираются таким образом, чтобы выполнялось условие ортогональности: , , , .

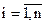Система для определения собственного вектора 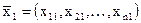, соответствующего собственному значению имеет вид:

(5.12)

В связи с тем, что собственный вектор определяется с точностью до числового множителя, предположим, что одна из компонент собственного вектора равна 1, т.е. . В итоге получаем систему нелинейных алгебраических уравнений с n неизвестными 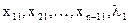, которую можно решать методом итерации:

(5.13)

Начальное приближение для системы (5.13) выбирается произвольно. Если метод итерации для системы (5.13) сходится, то для достаточно больших значений k можно приближенно положить , .

Для определения и воспользуемся двумя соотношениями: 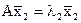и условием ортогональности векторов и :

(5.14)

где .

Учитывая, что определяется с точностью до числового множителя, положим . Исключив из (5.14) уравнение для определения и получим систему из (n-1) – го нелинейного алгебраического уравнения для определения неизвестных . Задавая произвольно начальное приближения, и решая систему методом итерации, получим:

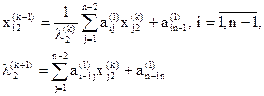(5.15)

Для контроля правильности вычисления можно воспользоваться уравнением:

.

Для определения и воспользуемся тремя соотношениями: и условиями ортогональности векторов и , а также векторов и . Далее процесс аналогичен процессу нахождения и и т.д.

Замечание: последующие собственные значения и векторы вычисляются с меньшей точностью, чем предыдущие.

Поиск по сайту: