Абсолютная и условная сходимость несобственных интегралов

Введем понятия абсолютной и условной сходимости интегралов. Пусть 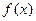интегрируема по любому сегменту .

Определение 1. Несобственный интеграл 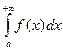называется абсолютно сходящимся, если сходится .

Определение2 Несобственный интеграл 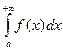называется условно сходящимся, если он сходится, а интеграл расходится.

Замечание. Положив в утверждении 2 , мы получим, что из абсолютной сходимости несобственного интеграла вытекает его сходимость.

Отметим, что утверждения 2 и 3 позволяют установить лишь абсолютную сходимость исследуемых несобственных интегралов.

Приведем еще один признак сходимости несобственного интеграла первого рода, пригодный для установления и условной сходимости этого интеграла.

Утверждение 4 (признак Дирихле – Абеля). Пусть выполнены следующие три условия:

1) функция 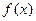непрерывна на полупрямой 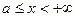и имеет на этой полупрямой ограниченную первообразную F(х);

2) функция определена и монотонно не возрастает на полупрямой 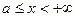и имеет равный нулю предел при ;

3) производная функции существует и непрерывна в каждой точке полупрямой 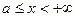. При выполнении трех условий несобственный интеграл

(2.1)

сходится.

Пример 1. Рассмотрим интеграл

. (2.2)

Полагая , , легко убедиться что для этого интеграла выполнены все условия утверждения 4. Поэтому интеграл (2.2) сходится.

Пример 2. Рассмотрим интеграл Френеля . Согласно п. 1 этого дополнения его сходимость вытекает из сходимости интеграла . Полагая , ,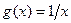легко убедимся, что выполнены все условия утверждения 4, Поэтому интеграл Френеля сходится.

Поиск по сайту: