Понятие абсолютно и условно сходящихся рядов

Теперь мы перейдем к изучению рядов, члены которых являются вещественными числами любого знака.

Определение1. Будем называть ряд

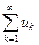(2.1)

абсолютно сходящимся, если сходится ряд

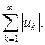(2.2)

Заметим, что в этом определении ничего не сказано о том, предполагается ли при этом сходимость самого ряда (2.1). Оказывается, такое предположение оказалось бы излишним, ибо справедлива следующая теорема.

Теорема 2. Из сходимости ряда (2.2) вытекает сходимость ряда (2.1).

Д о к о з а т е л ь с т в о. Воспользуемся критерием Коши для ряда. Требуется доказать, что для любого найдется номер N такой, что для всех номеров n, удовлетворяющих условию n N, и для любого натурального p справедливо неравенство

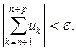(2.3)

Фиксируем любое . Так как ряд (2.2) сходится, то в силу критерия Коши найдется номер N такой, что для всех номеров n, удовлетворяющих условию n N, и для любого натурального p справедливо неравенство

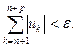(2.4)

Так как модуль суммы нескольких слагаемых не превосходит суммы их модулей, то

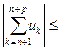
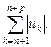(2.5)

Сопоставляя неравенства (2.4) и (2.5). получим неравенство (2.3). Теорема доказана.

Определение 2. Ряд (2.1) называетсяу с л о в н о с х о д я щ и м с я, если этот ряд сходится, в то время как соответствующий ряд из модулей расходится.

Поиск по сайту: