Ряд Тейлора

Определение 3.1. Пусть функция определена в некоторой окрестности точки и имеет в этой точке производные всех порядков. Тогда ряд

(3.1)

называется рядом Тейлора функции в точке .

Возникает вопрос: когда ряд Тейлора (3.1) функции на некотором интервале сходится к ? Чтобы исследовать этот вопрос, напишем формулу Тейлора для функции

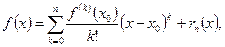(3.2)

которая справедлива при любом . В этой формуле обозначает остаточный член формулы Тейлора. Полагая

перепишем формулу (3.2) в виде

, (3.3)

где - -я частичная сумма ряда Тейлора.

Отсюда видно, что, для того чтобы функция равнялась на рассматриваемом интервале сумме своего ряда Тейлора, т.е. чтобы

,

необходимо и достаточно, чтобы для всех из этого интервала

, (3.4)

Если это имеет место, то из формулы (3.3) следует, что остаточный член формулы Тейлора является также и суммой -го остатка ряда Тейлора (3.1).

Укажем теперь одно достаточное условие разложимости функции в степенной ряд.

Теорема 8. Пусть функция и все ее производные ограничены в совокупности на интервале , т.е. существует такая постоянная 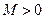, что для всех и всех выполняется неравенство

, (3.5)

Тогда на интервале функция раскладывается в ряд Тейлора, т.е.

, (3.6)

Доказательство. Прежде всего, заметим, что, каково бы ни было число ,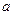

, (3.7)

Действительно, пусть 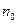такое, что

,

Тогда при всех

,

и поэтому

,

где правая часть неравенства стремится к нулю при , откуда и следует равенство (3.7). Это равенство следует и непосредственно из того, что выражение является общим членом сходящегося ряда . Для того, чтобы доказать формулу (3.,6) достаточно убедиться, что

, (3.4)

где - остаточный член в формуле Тейлора функции . Возьмем в форме Лагранжа. Из неравенств (3.5) следует, что

,

где . Поскольку в силу (3.7)

,

то при выполняется условие (3.4)

Теорема доказана.

Поиск по сайту: