Определение ряда и его сходимость

В настоящем параграфе понятие суммы обобщается на некоторые случаи бесконечного числа слагаемых и изучаются свойства таких сумм. Многие из рассматриваемых ниже вопросов справедливы не только для вещественных чисел, но и для комплексных чисел. Поэтому в отличие от предыдущих глав в настоящей главе будем вести рассмотрения в комплексной области.

Определение 1. Пусть задана последовательность комплексных чисел 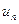, n= 1, 2, ….. составим новую последовательность чисел , n= 1, 2, …, следующим образом:

.........

.........

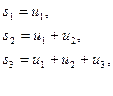
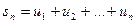
Последовательность 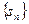называется рядом (подробнее: рядом с общим членом 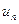) и обозначается

(1.1)

или

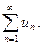(1.2)

Элементы исходной последовательности называются членами ряда (1.1), а элементы последовательности 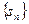– частичными суммами этого ряда, при этом член 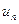называется n-м членом ряда, а конечная сумма – n-й частичной суммой ряда, n=1, 2, …,

Определение 2. Ряд

(1.3)

членами которого являются члены ряда (1.1), начиная с (n+1)- го, взятые в том же порядке, что и в данном ряде, называется n-м остатком ряда (1.1).

Поскольку ряд является последовательностью, а именно последовательностью своих частичных сумм, то он, как и всякая последовательность, может сходиться или расходиться. В первом случае он называется сходящимся рядом, а во втором – расходящимся.

Определение 3. Если ряд (1.1) сходится, то предел

называется его суммой.

В этом случае пишут

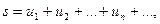
или

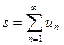. (1.4)

Таким образом, мы будем употреблять один и тот же символ 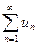как для обозначения самого ряда (1.1), так и для обозначения его суммы, если он сходится.

Если

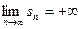, или , или ,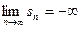

то соответственно пишут

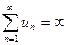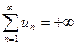, или .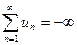

задаче изучения сходимости последовательностей.

.

Если остаток (1.3) ряда (1.1) сходится, то его сумму будем обозначать :

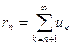, (1.5)

и называть для краткости просто остатком ряда.

Всякую сумму конечного числа слагаемых

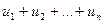
можно рассматривать как ряд, добавив к ней члены

Сумма получившегося ряда, очевидно, будет совпадать с заданной суммой, ибо при всех 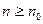его частичные суммы равны .

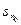Если заранее неизвестно, содержит сумма конечное или бесконечное число слагаемых, то иногда удобно в обоих случаях называть ее рядом, считая, что конечная сумма является рядом в вышеуказанном смысле.

Поиск по сайту: