Признаки Даламбера и Коши

К признакам сравнения непосредственно примыкают два весьма употребительных признака сходимости рядов с положительными членами- признаки Даламбера и Коши, которые основаны на сравнении рассматриваемого ряда с рядом, составленным из элементов геометрической прогрессии, а именно со сходящимся рядом

q^k=q+q²+...+q^k+..., q <1, (3.1)

или с расходящимся рядом

k =1+1+...+1... (3.2)

Теорема (признак Даламбера) 4.1. Если для всех номеров по крайней мере начиная с некоторого номера, справедливо неравенство

(3.3)

то ряд 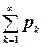сходится (расходится).

4.2. Если существует предел

, (3.4)

то ряд 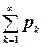сходится приL < 1 и расходится при L>1.

Теорему 4. 2 обычно называют признаком Даламбера в предельной форме. В этой форме он наиболее часто используется.

Доказательство. Докажем отдельно теорему 4. 1

Для доказательства теоремы 4.1положим 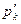= q^k
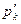( =1). Тогда , где q <1( =1) и мы можем переписать равенство (3.3) в виде

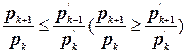. (3.5)

Так как ряд совпадающий с рядом (3.1) (3.2), сходится (расходится), то неравенство (3.5) на основании теоремы сравнения 3 гарантирует сходимость (расходимость) ряда Теорема 4.1 доказана.

Теорема (признак Коши )5.1. Если для всех номеров k, по крайней мере начиная с некоторого номера, справедливо неравенство

q<1 ( 1) (3.6)

то ряд 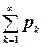сходится (расходится).

5.2. Если существует предел

(3.7)

то ряд 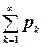сходится при L<1 и расходится при L>1

Теорему 5. 2 обычно называют признаком Коши в предельной форме.

Доказательство. Докажем отдельно теорему 5. 1.

Для доказательства теоремы 5. 1 положим 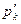= q^k

Тогда из неравенства (3.6) получим

(3.8)

Так как совпадающий с рядом (3.1) ((3.2)) сходится (расходится), то неравенство (3.8) на основании теоремы сравнения 2 гарантирует сходимость (расходимость) ряда 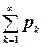. Теорема 5.1 доказана.

4. Интегральный признак Коши-Маклорена

Признаки Даламбера и Коши оказываются непригодными для выяснения вопроса о сходимости некоторых часто встречающихся рядов с положительными членами. Так, например, с помощью этих признаков нельзя выяснить вопрос о сходимости обобщенного гармонического ряда

(4.1)

( - любое вещественное число).

Установлено, что при α<1 ряд (4.1) расходится, однако остается открытым вопрос о сходимости этого ряда при α>1. В этом пункте мы установим еще один общий признак сходимости ряда с неотрицательными членами, из которого, в частности будет вытекать сходимость ряжа(4.1) при α>1.

Теорема 6(признак Коши-Маклорена). Пусть функция f(x)неотрицательна и не возрастает всюду на полупрямой x>m, где m-любой фиксированный номер. Тогда числовой ряд

=f(m)+f(m+1)+f(m+2)+.... (4.2)

сходится в том и только в том случае, когда существует предел при n последовательности

a_n= (4.3)

Доказательство. Пусть k- любой номер, удовлетворяющий условию k m+1 а х - любое значение аргумента из сегмента k-1 x k. Так как по условию функции не возрастает на указанном сегменте, то для всех х из указанного сегмента справедливы неравенства

f(x) . (4.5)

Функция f(x), будучи ограниченной и монотонной, интегрируема на сегменте [ k-1,k ]. Более того, из неравенства (4.5) и из свойства рядов вытекает, что

,

или

f(k) (4.6)

Эти неравенства установлены нами для любого . Запишем их для значений k, равных m+1,m+2,...,n, где n- любой номер, превосходящий m:

,

,

....................................................

_.

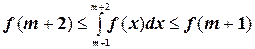Складывая почленно записанные неравенства, получим

(4.7)

Договоримся обозначать символ S_n n -ю частичную суму ряда (4.2), равную

S _n= (4.8)

Приняв это обозначение и учитывая обозначение (4.3), мы можем следующим образом переписать неравенства(4.7):

(4.8)

Эти неравенства позволяют без труда доказать теорему. В самом деле, из формулы (4.3)очевидно, что последовательность{ a_n } является неубывающей. Следовательно для сходимости этой последовательности необходима и достаточна ее ограниченность. Для сходимости ряда (4.2) в силу теоремы 1 необходима и достаточна ограниченность последовательности { S_n }. Из неравенства (4.8) вытекает, что последовательность { S_n } ограничена тогда и только тогда, когда ограничена последовательность { a_n }. Теорема доказана.

Литература: 1,с. 12-25; 7, с.262-272; 10,с. 507-521

Контрольные вопросы:

1. Какой ряд называется рядом с неотрицательными членами?

2. Сформулируйте необходимое и достаточное условие сходимости ряда.

3. Сформулируйте признаки сравнения.

4. Исследуйте вопрос о сходимости ряда , где b>0.

5. Исследуйте вопрос о сходимости обобщенного гармонического ряда.

6. Сформулируйте и докажите признак Даламбера.

7. Сформулируйте и докажите признак Даламбера в предельной форме.

8. Сформулируйте и докажите признак Коши.

9. Сформулируйте и докажите признак Коши в предельной форме.

10.Сформулируйте и докажите интегральный признак Коши- Маклорена.

Поиск по сайту: