Равномерная сходимость последовательностей и рядов

Определение 2.1. Пусть задана последовательность функций (1.1) и функция f, определенная на множестве Е. Будем говорить, что указанная последовательность сходится к функции f равномерно на множестве Е, если для любого существует такой номер 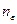, что если 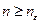, то для всех 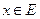выполняется неравенство

(2.1)

Последовательность (1.1) называется равномерно сходящейся на множестве Е, если существует функция f, к которой она рав­номерно сходится на Е.

Очевидно, что если последовательность (1.1) равномерно схо­дится к функции f на множестве Е, то она и просто сходится к этой функции на Е.

Если последовательность { 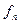} сходится на множестве Е к фун­кции f, то мы будем это символически записывать следующим образом:

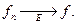на Е

Если же эта последовательность { 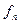} равномерно сходится на Е к функции f, то будем писать 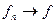на Е равномерно

Заметим, что если последовательность (1.1) просто сходится к функции f на множестве Е, то это означает, что для любого и любого 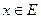существует номер 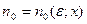, зависящий как от 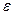, так и от х, такой, что для всех номеров 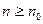имеет место неравенство (2.1).

Сущность равномерной сходимости последовательности функ­ций состоит в том, что для любого можно выбрать такой номер , зависящий только от заданного 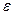и не завися­щий от выбора точки 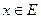, что при неравенство (2.1) будет выполняться всюду на множестве Е, т. е. «графики» функ­ций 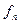будут расположены в « 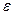-полоске», окружающей график функции f (рис. 1).

Таким образом, в случае равномерной сходимости для любого при всех достаточно больших n (именно при ) значения функций 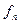приближают функцию f с погрешностью мень­шей 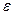,сразу на всем множестве Е.

Ряд 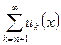(2.2)

называется n-м остатком ряда. Он сходится на Е тогда и только тогда, когда на Е сходится сам ряд (2.1). Если в этом случае сумму ряда (2.2) обозначить через 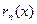, то

s

Как и в случае числовых рядов, согласно определению, каж­дый функциональный ряд является последовательностью своих частичных сумм:

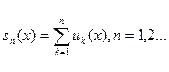
При этом для каждой функциональной последовательности (1.1) существует ряд (2.2), для которого она является после­довательностью его частичных сумм. Члены этого ряда определяются однозначно:

Это обстоятельство дает возможность перефразировать всякую теорему, доказанную для функциональных рядов, в соответству­ющую теорему для функциональных последовательностей, и на­оборот. Мы неоднократно будем использовать это обстоятельство.

Теорема 1 (критерий Коши равномерной сходимости последовательностей). Для того чтобы последовательность функций 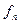, , 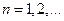определенных на некотором множестве Е, равно­мерно сходилась на этом множестве, необходимо и достаточно, чтобы для любого существовал такой номер , что для всех номеров , всех целых 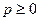и всех точек 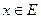выпол­нялось неравенство

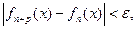(2.3)

Часто бывает полезным следующее простое достаточное условие равномерной сходимости функциональных последовательностей.

Теорема 2 (признак Вейерштрасса). Пусть задана последовательность { }. Если существует такая числовая последовательность { }, что

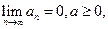(2.4)

и для всех 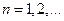, и всех 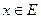выполняется неравенство

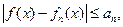(2.5)

то последовательность { 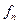} равномерно на Е сходится к функции f.

Доказательство. В силу условия (2.4) для любого существовал такой номер , что для всех номеров выполняется неравенство

.

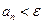Но тогда в силу условия (2.5) для всех и всех 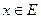выпол­няется неравенство

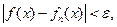
а это и означает равномерную сходимость последовательности { } к функции 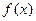на множестве Е.

Для рядов, естественно, также можно ввести понятие равномерной сходимости.

Определение 2.2 Ряд

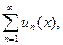(2.6)

члены которого являются функциями, определенными на множе­стве Е, называется равномерно сходящимся на этом множестве, если последовательность его частичных сумм равномерно сходится на Е.

Таким образом, равномерная сходимость ряда (2.6) означает существование такой функции 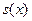, что

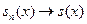равномерно на Е (2.7)

Поскольку из (2.7) следует, что 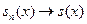на Е, то 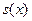является суммой ряда (2.6).

Положим

Тогда 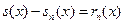и условие (2.7) можно переписать в эквивалентной форме:

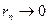равномерно на Е (2.9)

откуда следует, что, для того чтобы сходящийся на Е ряд (2.6) равномерно сходился на множестве Е, необходимо и достаточно, чтобы

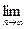
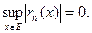(2.10)

Таким образом, из равномерной сходимости ряда, в частности, вытекает, что, начиная с некоторого номера верхние грани

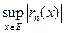
конечны, а условие (2.10) сводит понятие равномерной сходи­мости ряда к стремлению к нулю числовой последовательности этих верхних граней.

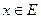Докажем эквивалентность условий (2.9) и (2.10). В самом деле, если имеет место (2.6), то для любого существует такой номер , что для всех номеров и всех точек выпол­нялось неравенство

Отсюда для всех

а это и означает выполнение условия (2.10).

Обратно, если выполнено условие (2.10) для любого существует такой номер , что для всех

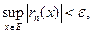
а значит, и подавно для всех и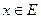

что и означает выполнение условия (2.9). Утверждение доказано.

Далее, замечая, что

из теоремы 1 получаем следующий критерий равномерной сходи­мости.

Поиск по сайту: