Следствие (необходимое условие равномерной сходимости ряда)

Если ряд (2.6) равномерно сходится на множестве Е, то

равномерно на Е (2.12)

Условие (2.12) получается из (2.11), если положить .

Часто бывает полезным следующий достаточный признак рав­номерной сходимости.

Теорема 4 (признак Вейерштрасса). Пусть даны два ряда: функциональный (2.6), членами которого являются функции определенные на множестве Е, и числовой

(2.13)

Если ряд (2.13) сходится и

(2.14)

то ряд (2.6) абсолютно и равномерно сходится на множестве Е.

Рассмотрим теперь достаточный признак равномерной сходимости, применимый в отличие от признака Вейерштрасса и к не абсолютно сходящимся рядам.

Теорема 5 (признак Дирихле). Пусть дан ряд

(2.15)

в котором функции и , , 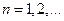определены на множестве Е и таковы, что

1) последовательность { } монотонна при каждом 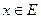и равномерно стремится к нулю на Е;

2) последовательность частичных сумм 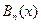, 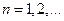ряда

ограничена на множестве Е.

Тогда ряд (2.15) равномерно сходится на множестве Е.

Теорема 6 (признак Абеля). Если:

1) последовательность { } ограничена на множестве Е:

,

и монотонно убывает или монотонно возрастает при каждом ,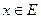

2) ряд

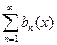
равномерно, сходится на множестве Е, то ряд (2.15) также равномерно сходится на Е.

Поиск по сайту: