 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Несобственные интегралы первого рода
Перенесем:понятиеопределенного интеграла на случай, когда область, по которой производится интегрирование, является бесконечной. На прямой 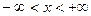 существует три типа бесконечных связных замкнутыхмножеств: 1) полупрямая
существует три типа бесконечных связных замкнутыхмножеств: 1) полупрямая 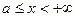 ; 2) полупрямая
; 2) полупрямая 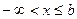 ;3)вся бесконечная прямая
;3)вся бесконечная прямая 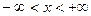 .
.
Ради определенности рассмотрим подробно первое из указанных множеств, т. е. полупрямую 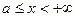 .
.
Предположим, что функция 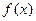 определена на полупрямой
определена на полупрямой 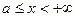 и что для любого числа А, удовлетворяющего неравенству
и что для любого числа А, удовлетворяющего неравенству 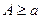 , существует определенный интеграл Римана
, существует определенный интеграл Римана 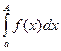 .
.
Этот определенный интеграл мы обозначим символом
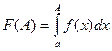 . (1.1)
. (1.1)
Естественно, возникает вопрос о существовании предела функции 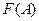 при
при 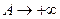
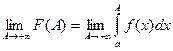 . (1.2)
. (1.2)
Определение1. Предел (1.2) в случае, если он существует, называется несобственным интегралом первого рода от функции 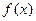 по полупрямой
по полупрямой 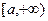 и обозначается символом
и обозначается символом
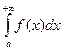 . (1.3)
. (1.3)
При этом говорят, что несобственный интеграл (1.3) сходится, и пишут равенство
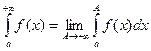 .
.
Впрочем, символ (1.3) употребляют и в случае, если указанного выше предела (1.2) не существует, но в этом случае говорят, что несобственный интеграл (1.3) расходится.
Совершенно аналогично определяются несобственные интегралы по полупрямой 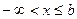 и по всей бесконечной прямой
и по всей бесконечной прямой 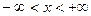 .
.
Первый из этих интегралов определяется как предел 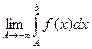 и обозначается символом
и обозначается символом  .
.
Что же касается интеграла  , то он определяется как предел
, то он определяется как предел
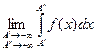
при независимом друг от друга стремлении 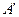 к
к 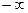 и
и 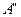 к
к  .
.
Из этих определений следует, что если для некоторого вещественного числа а сходится каждый из несобственных интегралов 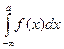 и
и 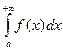 , то сходится и несобственный интеграл
, то сходится и несобственный интеграл  , причем справедливо равенство
, причем справедливо равенство
 =
= 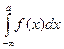 +
+ 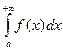 .
.
Заметим еще, что если сходится несобственный интеграл 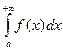 и b – любое число, превосходящее, то сходится и несобственный интеграл
и b – любое число, превосходящее, то сходится и несобственный интеграл 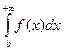 , причем
, причем 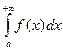 =
= 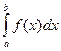 +
+ 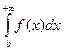 .Это утверждение непосредственно вытекает из определения сходимости несобственного интеграла.
.Это утверждение непосредственно вытекает из определения сходимости несобственного интеграла.
Поиск по сайту: