Дифференциальные уравнения первого порядка

Дифференциальные уравнения 1-го порядка имеют вид

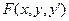=0 или

Если уравнение (1) удастся разрешить относительно , то мы получим

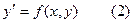
- уравнение первого порядка, разрешенное относительно производной.

Будем считать, что функция 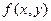задана на некотором открытом множестве .

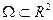Общим решением дифференциального уравнения (2) называется функция

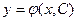такая, что:

1) она удовлетворяет уравнению (2) при значениях постоянной 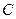, принадлежащих некоторому определенному множеству; (это множество определяется уравнением (2)).

2) какова бы ни была точка 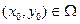, найдется такое значение 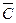постоянной 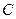, что функция 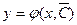будет удовлетворять условию .

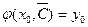Соотношение вида , неявно определяющее общее решение, называется общим интегралом дифференциального уравнения первого порядка.

Соотношение, получаемое из общего интеграла при конкретном значении постоянной 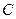, называется частным интегралом дифференциального уравнения.

Имеет место следующая теорема существования и единственности решения дифференциального уравнения (2).

Теорема 1. Пусть функция 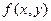определена и непрерывна на открытом множестве 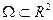, 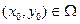. Тогда через точку 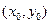проходит по крайне мере одна интегральная кривая. Если функция 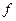имеет на непрерывную частную производную по переменной , то существует единственное решение 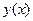уравнения (2), удовлетворяющее условию .

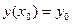Условие 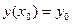называют начальным условием. Задачу отыскания решения уравнения (2), удовлетворяющего начальному условию 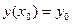, называют задачей Коши.

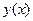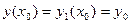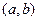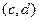Единственность решения задачи Коши надо понимать в том смысле, что если и есть два решения задачи Коши, удовлетворяющие одному и тому же начальному условию , заданные соответственно на интервалах и , то 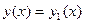на пересечении этих интервалов.

Уравнение (2) в каждой точке 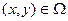определяет , то есть угловой коэффициент касательной к интегральной кривой, проходящей через эту точку. Поэтому задача интегрирования дифференциального уравнения (2) геометрически может быть истолкована следующим образом: от каждой точки 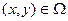отложим вектор, образующий с осью 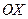угол 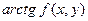; получим некоторое поле направлений; требуется провести кривые так, чтобы расставленные стрелки показывали в каждой точке направление касательной.

Изоклиной дифференциального уравнения (2) называется геометрическое место точек, в которых касательные к интегральным кривым имеют одно и то же направление.

Семейство изоклин определяется уравнением где – параметр. Строя достаточно густую сеть изоклин, т.е. давая близкие числовые значения, мы можем достаточно точно построить интегральную кривую

дифференциального уравнения (2).

Не существует общего метода решения дифференциального уравнения первого порядка. Далее мы выделим некоторые типы дифференциальных уравнений, для которых можно дать метод решения.

Поиск по сайту: