АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений

Читайте также:
  1. BRP открывает новый виток инновационного развития с выпуском платформы Ski-Doo REV
  2. II ОБЩИЕ НАЧАЛА ПУБЛИЧНО-ПРАВОВОГО ПОРЯДКА
  3. II. Вопросительное предложение
  4. II. ЦЕЛИ И ФОРМЫ ДЕЯТЕЛЬНОСТИ ПРИХОДА
  5. IV. Формы контроля
  6. IV. Формы контроля
  7. IV.1. Общие начала частной правозащиты и судебного порядка
  8. V. Формы контроля
  9. VII Формы текущего и итогового контроля
  10. VII. Вопросник для анализа учителем особенностей индивидуального стиля своей педагогической деятельности (А.К. Маркова)
  11. VII. Новые формы российского предпринимательства
  12. X. примерный перечень вопросов к итоговой аттестации

Эллипсоид (рис. 4.18)

Каноническое уравнение:

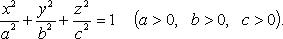
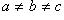- трехосный эллипсоид;

- эллипсоид вращения вокруг оси Oz;

- эллипсоид вращения вокруг оси Oy;

- эллипсоид вращения вокруг оси Ox;

- сфера.

Сечения эллипсоида плоскостями - либо эллипс (окружность), либо точка, либо .


Конус второй степени (рис. 4.19)

Каноническое уравнение:

a = b - конус вращения (прямой круговой).

Сечения конуса плоскостями: в плоскости, пересекающей все прямолинейные образующие, - эллипс; в плоскости, параллельной одной прямолинейной образующей, - парабола; в плоскости, параллельной двум прямолинейным образующим, - гипербола; в плоскости, проходящей через вершину конуса, - пара пересекающихся прямых или точка (вершина).

Эллиптический цилиндр (рис. 4.24)

Каноническое уравнение:

при a = b - круговой цилиндр.

Гиперболический цилиндр (рис. 4.25)

Каноническое уравнение:


Параболический цилиндр (рис. 4.26)

Каноническое уравнение:

Вопрос25 поверхности второго порядка (гиперболоиды, параболоиды) и их канонические уравнения.

Однополостный гиперболоид (рис. 4.20)

Каноническое уравнение:

a = b - однополостный гиперболоид вращения вокруг оси Oz.

Горловой эллипс:

Асимптотический конус:

Сечения однополостного гиперболоида плоскостями - либо эллипс, либо парабола, либо гипербола, либо пара прямых (прямолинейных образующих).

 

Двуполостный гиперболоид (рис. 4.21)

Каноническое уравнение:

a = b - двуполостный гиперболоид вращения вокруг оси Oz.

Асимптотический конус:

Сечения двуполостного гиперболоида плоскостями: либо эллипс, либо гипербола, либо парабола, либо точка, либо .


Эллиптический параболоид (рис. 4.22)

Каноническое уравнение:

p = q - параболоид вращения вокруг оси Oz.

Сечения эллиптического параболоида плоскостями - либо эллипс, либо парабола, либо точка, либо .

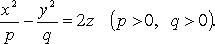
Гиперболический параболоид (рис. 4.23)

Каноническое уравнение:

Сечения гиперболического параболоида плоскостями - либо гипербола, либо парабола, либо пара прямых (прямолинейных образующих).

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)