Линейные операции над матрицами

1. Сложение матриц.

Определение 3.4. Суммой матриц А и В одинаковой размерности m n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах:

Свойства сложения:

1. А + В = В + А.
2. (А + В) + С = А + (В + С).
3. Если О – нулевая матрица, то А + О = О + А = А

Замечание 1. Справедливость этих свойств следует из определения операции сложения матриц.

Замечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности.

Пример.

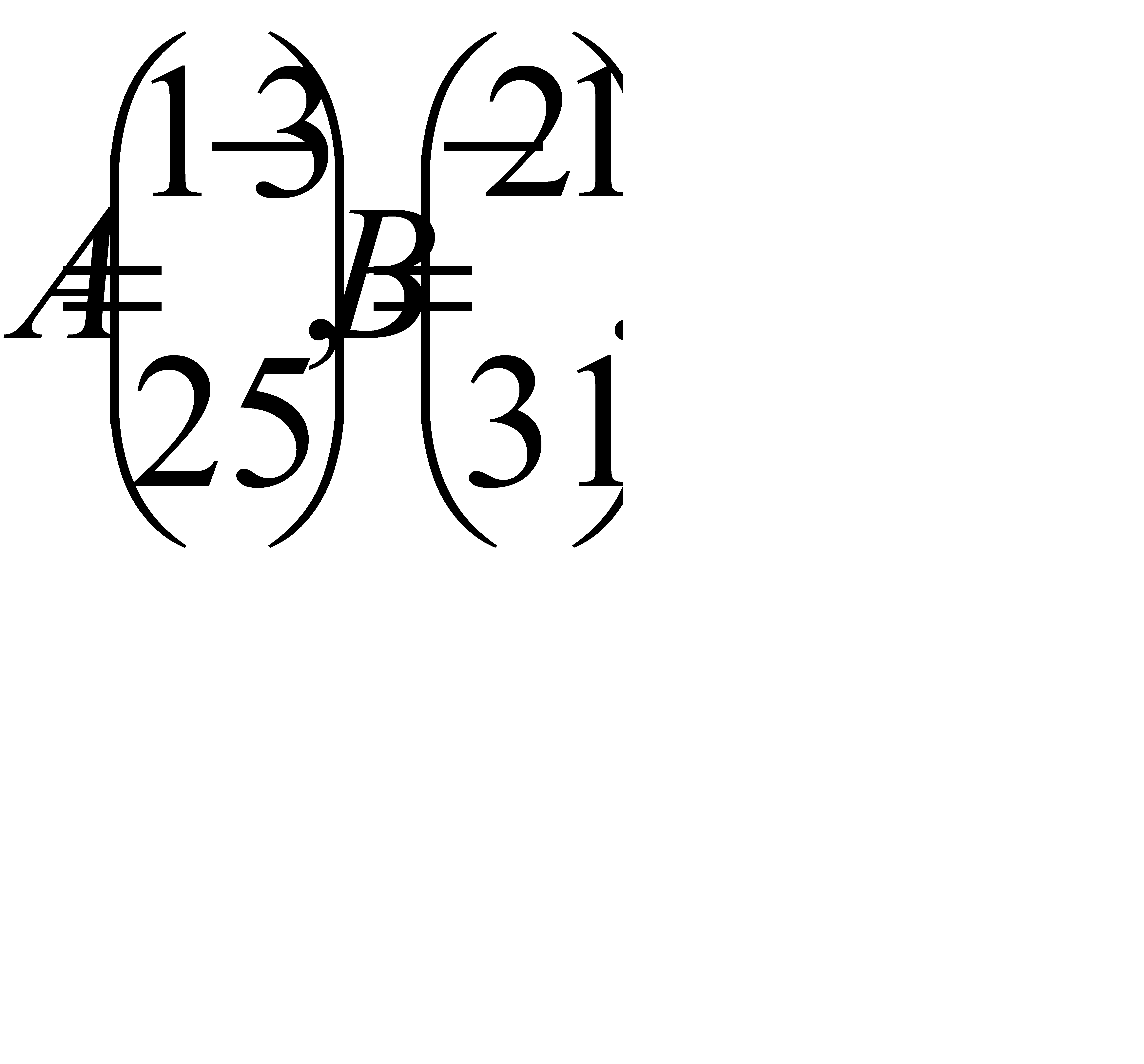
2. Умножение матрицы на число.

Определение 3.5. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.

Свойства умножения матрицы на число:

1. (km)A=k(mA).
2. k(A + B) = kA + kB.
3. (k + m)A = kA + mA.

Замечание 1. Справедливость свойств следует из определений 3.4 и 3.5.

Замечание 2. Назовем разностью матриц А и В матрицу С, для которой С + В =А, т.е. С = А + (-1)В.

Пример.

. Тогда

Поиск по сайту: