 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Свойства линейно зависимых и линейно независимых векторов
1. Если в систему векторов входит нулевой вектор, то она линейно зависима
.
2. Если в системе векторов имеется два равных вектора, то она линейно зависима.
3. Если в системе векторов имеется два пропорциональных вектора  , то она линейно зависима.
, то она линейно зависима.
4. Система из  векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.
векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.
5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.
6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.
7. Если система векторов  линейно независима, а после присоединения к ней вектора
линейно независима, а после присоединения к ней вектора  оказывается линейно зависимой, то вектор
оказывается линейно зависимой, то вектор  можно разложить по векторам
можно разложить по векторам  , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.
, и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.
Докажем, например, последнее свойство. Так как система векторов 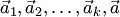 — линейно зависима, то существуют числа
— линейно зависима, то существуют числа  , не все равные 0, что. В этом равенстве
, не все равные 0, что. В этом равенстве  . В самом деле, если
. В самом деле, если  , то
, то  . Значит, нетривиальная линейная комбинация векторов
. Значит, нетривиальная линейная комбинация векторов  равна нулевому вектору, что противоречит линейной независимости системы
равна нулевому вектору, что противоречит линейной независимости системы  . Следовательно,
. Следовательно,  и тогда
и тогда  , т.е. вектор
, т.е. вектор  есть линейная комбинация векторов
есть линейная комбинация векторов  . Осталось показать единственность такого представления. Предположим противное. Пусть имеется два разложения
. Осталось показать единственность такого представления. Предположим противное. Пусть имеется два разложения  и
и  , причем не все коэффициенты разложений соответственно равны между собой (например,
, причем не все коэффициенты разложений соответственно равны между собой (например,  ).
).
Тогда из равенства  получаем
получаем  .
.
Следовательно, линейная комбинация векторов  равна нулевому вектору. Так как не все ее коэффициенты равны нулю (по крайней мере
равна нулевому вектору. Так как не все ее коэффициенты равны нулю (по крайней мере  ), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов
), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов  . Полученное противоречие подтверждает единственность разложения.
. Полученное противоречие подтверждает единственность разложения.
Векторное пространство 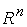 называется n -мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит.
называется n -мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит.
Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов.
Пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным.
Совокупность n линейно независимых векторов n - мерного векторного пространства 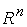 называется его базисом.
называется его базисом.
Если каждой паре векторов x, y линейного пространства L поставлено в соответствие действительное число (x, y), так, что для любых x, y и z из L и любого действительного числа α справедливы следующие аксиомы:
(x, y) = (y, x),
(α ·x, y) = α ·(x, y),
(x + y, z) = (x, z) + (y, z),
(x, x) > 0 при x ≠ 0, (0, 0) = 0,
то в пространстве L определено скалярное произведение (x, y).
Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством.
| Теорема 1 (неравенство Коши-Буняковского) |
Для любых чисел 
 . .
|
| Доказательство |
При  неравенство неравенство  верно. Допустим, верно. Допустим,
 .
Докажем, что .
Докажем, что
  .
Перепишем это неравенство, частично раскрыв скобки: .
Перепишем это неравенство, частично раскрыв скобки:
  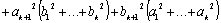 .
Легко заметить, что для того, чтобы доказать это неравенство, достаточно доказать .
Легко заметить, что для того, чтобы доказать это неравенство, достаточно доказать
 Перенеся все слагаемые в одну сторону, и сгруппировав их, получаем очевидное неравенство:
Перенеся все слагаемые в одну сторону, и сгруппировав их, получаем очевидное неравенство:
 А это и доказывает неравенство Коши-Буняковского.
А это и доказывает неравенство Коши-Буняковского.
|
| Определение 2 |
1. Число  называется средним арифметическим чисел называется средним арифметическим чисел  .
2. Если .
2. Если 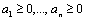 , то число , то число  называется средним геометрическим чисел называется средним геометрическим чисел  . .
|
| Теорема 3 (неравенство Коши) |
Пусть 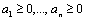 , тогда , тогда
  . (1) . (1)
|
| Доказательство |
Шаг первый: сначала индукцией докажем это неравенство для натуральных чисел вида  . При m=1 надо доказать, что . При m=1 надо доказать, что  . Это неравенство эквивалентно . Это неравенство эквивалентно  , то есть , то есть  . Последнее неравенство верно, значит, и первоначальное верно, так как они равносильны. Допустим, неравенство верно при m=k, то есть . Последнее неравенство верно, значит, и первоначальное верно, так как они равносильны. Допустим, неравенство верно при m=k, то есть
 . (2)
Докажем неравенство (1) для m=k+1, то есть докажем, что . (2)
Докажем неравенство (1) для m=k+1, то есть докажем, что
 .
В самом деле, .
В самом деле,     .
Итак, мы доказали неравенство Коши, когда количество чисел в средних есть степень двойки. А как быть с остальными? Для них мы докажем неравенство Коши, используя еще одну модификацию индукции – "индукцию вниз". Допустим, что неравенство Коши верно для n=k, то есть допустим, что .
Итак, мы доказали неравенство Коши, когда количество чисел в средних есть степень двойки. А как быть с остальными? Для них мы докажем неравенство Коши, используя еще одну модификацию индукции – "индукцию вниз". Допустим, что неравенство Коши верно для n=k, то есть допустим, что
 , (3)
и докажем это неравенство для n=k-1. Для этого в неравенстве Коши положим , (3)
и докажем это неравенство для n=k-1. Для этого в неравенстве Коши положим  , тогда (3) будет иметь вид: , тогда (3) будет иметь вид:
 После элементарных алгебраических преобразований получили:
После элементарных алгебраических преобразований получили:
 .
Сократим неравенство на второй множитель правой части: .
Сократим неравенство на второй множитель правой части:
 .
И, наконец, возведем обе части неравенства в степень .
И, наконец, возведем обе части неравенства в степень  : :
 .
Неравенство Коши доказано полностью. .
Неравенство Коши доказано полностью.
|
Поиск по сайту: