Свойства функций, непрерывных на отрезке

Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M  f(x)  M.

Доказательство этого свойства основано на том, что функция, непрерывная в точке х₀, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х₀, то образуется некоторая окрестность точки х₀.

Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.

Т.е. существуют такие значения х₁ и х₂, что f(x₁) = m, f(x₂) = M, причем

m  f(x)  M

Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).

Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.

Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.

Найдём частные производные функции Примеры скриптов для клиента на языке JavaScript

Свойство 4: Если функция f(x) непрерывна в точке х = х₀, то существует некоторая окрестность точки х₀, в которой функция сохраняет знак.

Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.

Т.е. если sign(f(a))  sign(f(b)), то  х₀: f(x₀) = 0.

Определение. Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого >0 существует >0 такое, что для любых точек х₁[a,b] и x₂[a,b] таких, что

х₂ – х₁< 

верно неравенство f(x₂) – f(x₁) < 

Отличие равномерной непрерывности от “обычной” в том, что для любого  существует свое , не зависящее от х, а при “обычной” непрерывности  зависит от  и х.

Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.

(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)

Пример.

Функция непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т.к. существует такое число >0 такое, что существуют значения х₁ и х₂ такие, чтоf(x₁) – f(x₂)>,  - любое число при условии, что х₁ и х₂ близки к нулю.

Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.

Найдём частные производные функции Примеры скриптов для клиента на языке JavaScript

Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода

у

Точки разрыва и их классификация.

Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х₀, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х₀ является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если односторонний предел (см. выше) , то функция называется непрерывной справа.

х₀

Если односторонний предел (см. выше) , то функция называется непрерывной слева.

Определение. Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

Гексаэдр - правильный шестигранник Вычислим интеграл Математика Задачи Ортогональная система координат в пространстве Математическая модель

Определение. Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х₀, достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Определение. Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)

не является непрерывной в любой точке х₀.

Пример. Функция f(x) = имеет в точке х₀ = 0 точку разрыва 2 – го рода, т.к.

.

Пример. f(x) =

Функция не определена в точке х = 0, но имеет в ней конечный предел , т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:

Гексаэдр - правильный шестигранник Вычислим интеграл Математика Задачи Ортогональная система координат в пространстве Математическая модель

График этой функции:

Пример. f(x) = =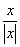

y

Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.

Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.

Непрерывность функции на интервале и на отрезке.

Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).

При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка

Поиск по сайту: