Примеры. Обозначим P(x) предикат «x делится на 5»

Обозначим P (x) предикат «x делится на 5». Используя квантор общности, можно формально записать следующие высказывания (конечно, ложные):

любое натуральное число кратно 5;

каждое натуральное число кратно 5;

все натуральные числа кратны 5;

следующим образом:

.

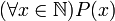Следующие (уже истинные) высказывания используют квантор существования:

существуют натуральные числа, кратные 5;

найдётся натуральное число, кратное 5;

хотя бы одно натуральное число кратно 5.

Их формальная запись:

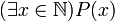.Введение в понятие

Пусть на множестве Х простых чисел задан предикат Р(х): «Простое число х — нечётно». Подставим перед этим предикатом слово «любое». Получим ложное высказывание «любое простое число х нечётно» (это высказывание ложно, так как 2 — простое чётное число).

Подставив перед данным предикатом Р(х) слово «существует», получим истинное выказывание «Существует простое число х, являющееся нечётным» (например, х=3).

Таким образом, превратить предикат в высказывание можно, поставив перед предикатом слова: «все», «существует», и др., называемые в логике кванторами.

Кванторы в математической логике

Высказывание 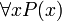означает, что область значений переменной x включена в область истинности предиката P (x).

(«При всех значениях (x) утверждение верно»).

Высказывание 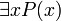означает, что область истинности предиката P (x) непуста.

(«Существует (x) при котором утверждение верно»).

Вопрос31 Граф и его элементы. Основные понятия. Инцидентность, кратность, петля, смежность. Типы графов. Маршрут в графе и его длина. Классификация маршрутов. Матрицы смежности ориентированного и неориентированного графов.

В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин.

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Ориентированным путём в орграфе называют конечную последовательность вершин v_i 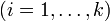, для которой все пары (v_i, v_{i + 1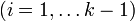}) являются (ориентированными) рёбрами.

Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u, v, u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:

Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины.

Всякий простой неэлементарный путь содержит элементарный цикл.

Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро).

Петля — элементарный цикл.

Граф или неориентированный граф G — это упорядоченная пара G: = (V, E), для которой выполнены следующие условия:

V это непустое множество вершин или узлов,

E это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

V (а значит и E, иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.

Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа.

Вершины u и v называются концевыми вершинами (или просто концами) ребра e = { u, v }. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.

Два ребра называются смежными, если они имеют общую концевую вершину.

Два ребра называются кратными, если множества их концевых вершин совпадают.

Ребро называется петлёй, если его концы совпадают, то есть e = { v, v }.

Степенью deg V вершины V называют количество инцидентных ей рёбер(при этом петли считают дважды).

Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

Ориентированный граф (сокращённо орграф) G — это упорядоченная пара G: = (V, A), для которой выполнены следующие условия:

V это непустое множество вершин или узлов,

A это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга ведёт от вершины v к вершине w.

Смешанный граф

Смешанный граф G — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой G: = (V, E, A), где V, E и A определены так же, как выше.

Ориентированный и неориентированный графы являются частными случаями смешанного.

Изоморфные графы(?)

Граф G называется изоморфным графу H, если существует биекция f из множества вершин графа G в множество вершин графа H, обладающая следующим свойством: если в графе G есть ребро из вершины A в вершину B, то в графе H должно быть ребро из вершины f (A) в вершину f (B) и наоборот — если в графе H есть ребро из вершины A в вершину B, то в графе G должно быть ребро из вершины f ^{− 1}(A) в вершину f ^{− 1}(B). В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента a_ij равно числу рёбер из i -й вершины графа в j -ю вершину.

Иногда, особенно в случае неориентированного графа, петля (ребро из i -й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента a_ii в этом случае равно удвоенному числу петель вокруг i -й вершины.

Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.

Поиск по сайту: