Матрицы и их классификация. Действия с матрицами. Экономические примеры

Классификация:

· Матрица, у которой все элементы выше (ниже) главной диагонали равны нулю, называются нижне- (верхнетреугольной) или просто треугольной;

· Матрица, у которой равное число строк и столбцов называют квадратной. Квадратная матрица размера 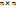называется квадратной матрицей порядка n;

· Квадратная матрица, у которой все элементы, кроме главной диагонали равны 0, называется диагональной;

· Диагональная матрица, у которой все элементы главной диагонали равны между собой, называется скалярной;

· Скалярная матрица, у которой все элементы главной диагонали равны 1, называют единичной матрицей и обозначают как Е;

· Матрица 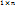называется вектор-строкой длины n, а матрица – вектор-столбцом длины n.

Если у матрицы поменять местами строки и столбцы, то такая матрица называется транспонированной.

Элементы матрицы, имеющие одинаковые индексы, образуют главную диагональ матрицы.

В отличии от умножения деление матрицы не определено, его заменяют умножением на обратную матрицу. Матрицу В называют обратной матрице А, если А*В=В*А=Е. Обратная матрица существует только у квадратной матрицы и то не всегда. Если обратной не существует, то про такую матрицу говорят что она вырождена или особенная.

Действия с матрицами:

1. Сложение (операция сложения вводится только для матриц одинаковых размеров);

2. Умножение на число;

3. Элементарные преобразования матриц:

a. Перестановка местами двух параллельных рядов;

b. Умножение всех элементов ряда матрицы на число, отличное от 0;

c. Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

4. Произведение матриц (операция умножения двух матриц вводится только для случая, когда число столбоцов первой матрицы равно числу строк второй матрицы).

Поиск по сайту: