 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Преобразование координат для прямоугольной системы координат
Получим формулы, связывающие координаты точки при переходе от одной прямоугольной системы координат к другой прямоугольной системе координат. Рассмотрим три типа преобразований:
а) параллельный перенос;
б) поворот системы координат;
в) зеркальное отражение в оси абсцисс (изменение направления оси ординат на противоположное).
Произвольный единичный (нормальный) вектор 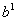 может быть записан следующим образом:
может быть записан следующим образом:
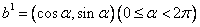 .
.
Единичный ортогональный (перпендикулярный) к 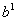 вектор, который мы обозначим через
вектор, который мы обозначим через 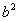 , может соответствовать только либо углу
, может соответствовать только либо углу 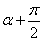 , либо
, либо 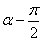 . Так как
. Так как
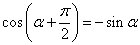 ,
, 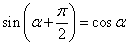 ,
,
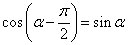 ,
, 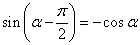 ,
,
то всевозможные ортонормированные системы 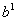 ,
, 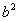 в
в 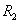 определяются либо равенствами (рис. 35)
определяются либо равенствами (рис. 35)
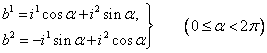 , (1')
, (1')
соответствующими вращению осей около начала на угол 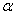 и сохранению ориентации, либо равенствами (рис. 36)
и сохранению ориентации, либо равенствами (рис. 36)
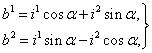 (1'')
(1'')
соответствующими вращению осей около начала на угол 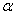 и изменению ориентации.
и изменению ориентации.
Оба преобразования объединяются в следующей формуле:
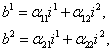 (1)
(1)
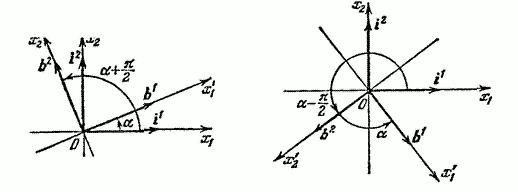
Рис. 35 Рис.36
где матрица преобразования
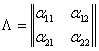 (2)
(2)
ортогональна (сумма квадратов элементов каждой из ее строк или столбцов равна 1, а скалярное произведение двух разных строк или столбцов равно 0).
Любое определенное ортогональное преобразование (1) есть на самом деле одно из преобразований (1'), (1") при некотором 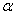 .
.
Из (1) в силу ортогональности матрицы (2) следует, что
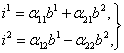 (3)
(3)
и мы получили преобразование, обратное преобразованию (1), с матрицей
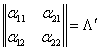 ,
,
сопряженной к 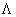 .
.
Зададим в плоскости произвольный вектор (точку) 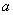 . Пусть он имеет в старой и новой системе координаты
. Пусть он имеет в старой и новой системе координаты 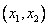 и
и 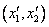 . Тогда
. Тогда
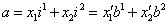 . (4)
. (4)
В силу формул (3) и (4)
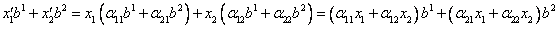 .
.
Поэтому, приравнивая компоненты при одинаковых ортах 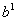 ,
, 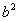 , получим
, получим
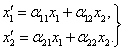 (5)
(5)
В силу же формул (1) и (4)
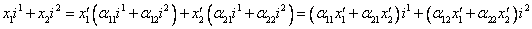 ,
,
откуда, приравнивая компоненты при 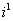 и
и 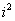 , получим формулы, обратные к (5):
, получим формулы, обратные к (5):
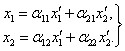 (6)
(6)
Если наряду с преобразованием (6) перенести еще начало осей 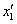 ,
, 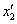 в точку
в точку 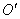 , имеющую координаты
, имеющую координаты 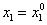 ,
, 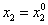 , то формулы (6) усложнятся, очевидно, следующим образом:
, то формулы (6) усложнятся, очевидно, следующим образом:
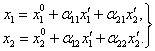 (7)
(7)
Итак, произвольное преобразование прямоугольных координат 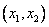 в прямоугольные координаты
в прямоугольные координаты 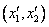 в точку
в точку 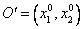 выражается формулами (7), где матрица
выражается формулами (7), где матрица
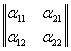
ортогональная.
Соответствующее преобразование, сохраняющее ориентацию системы координат, имеет вид
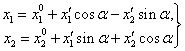 (7')
(7')
и преобразование, меняющее ориентацию, имеет вид
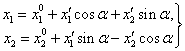 (7'')
(7'')
(матрицы коэффициентов при 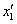 и
и 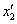 в (7') и (7") соответственно транспонируют (1') и (1"))
в (7') и (7") соответственно транспонируют (1') и (1"))
7. Алгебраическая линия и её порядок. Теорема об инвариантности порядка
Напомним, что многочленом степени 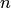 одной переменной
одной переменной 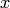 называется выражение вида
называется выражение вида
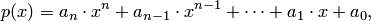
где 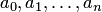 — действительные числа (коэффициенты многочлена),
— действительные числа (коэффициенты многочлена), 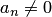 — старший коэффициент,
— старший коэффициент, 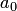 — свободный член. Степень многочлена обозначается
— свободный член. Степень многочлена обозначается 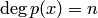 .
.
Многочленом двух переменных 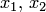 называется выражение вида
называется выражение вида
где 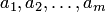 — действительные числа (коэффициенты многочлена),
— действительные числа (коэффициенты многочлена), 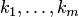 и
и 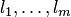 — целые неотрицательные числа. Число
— целые неотрицательные числа. Число
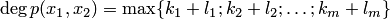
называется степенью многочлена двух переменных.
Алгебраической линией на плоскости называется множество точек, которое в какой-либо аффинной системе координат 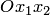 может быть задано уравнением вида
может быть задано уравнением вида
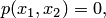
| (3.4) |
где 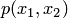 — многочлен двух переменных
— многочлен двух переменных 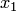 и
и 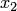 .
.
Уравнение вида (3.4) называется алгебраическим уравнением с двумя неизвестными. Степенью уравнения (3.4) называется степень многочлена 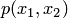 . Одна и та же линия может быть задана уравнением вида (3.4) с многочленами разных степеней. Порядком алгебраической линии называется наименьшая из степеней этих многочленов.
. Одна и та же линия может быть задана уравнением вида (3.4) с многочленами разных степеней. Порядком алгебраической линии называется наименьшая из степеней этих многочленов.
Всякую неалгебраическую линию называют трансцендентной.
Теорема об инвариантности порядка алгебраической линии
Если в некоторой аффинной системе координат на плоскости линия задана уравнением (3.4), то и в любой другой аффинной системе координат эта линия задается уравнением того же вида (3.4) и той оке степени.
Действительно, пусть в аффинной системе координат 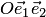 уравнение имеет вид (3.4):
уравнение имеет вид (3.4):
Получим уравнение этой линии в другой (новой) аффинной системе координат 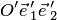 . Старые координаты точки связаны с новыми ее координатами выражениями (2.8):
. Старые координаты точки связаны с новыми ее координатами выражениями (2.8):
где 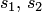 — координаты вектора переноса начала координат
— координаты вектора переноса начала координат 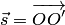 , а
, а 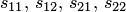 — элементы матрицы перехода базиса
— элементы матрицы перехода базиса 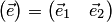 к новому. Подставим эти выражения в одночлен
к новому. Подставим эти выражения в одночлен 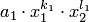 :
:
Раскрывая скобки, получаем многочлен двух переменных 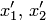 , степень которого не больше, чем
, степень которого не больше, чем 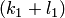 . Аналогичные многочлены получим из других одночленов, входящих в левую часть (3.4). Сложив эти многочлены, получим многочлен
. Аналогичные многочлены получим из других одночленов, входящих в левую часть (3.4). Сложив эти многочлены, получим многочлен 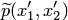 , степень которого не превосходит степени исходного многочлена
, степень которого не превосходит степени исходного многочлена 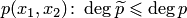 . Таким образом, при замене системы координат порядок алгебраической линии не увеличивается. Но он не может и уменьшиться, так как если порядок уменьшится при переходе к новой системе координат, то он должен увеличиться при обратном переходе к старой системе координат. Следовательно, порядок алгебраической линии остается неизменным в любой аффинной системе координат (говорят, что порядок алгебраической линии является инвариантом). Теорема доказана.
. Таким образом, при замене системы координат порядок алгебраической линии не увеличивается. Но он не может и уменьшиться, так как если порядок уменьшится при переходе к новой системе координат, то он должен увеличиться при обратном переходе к старой системе координат. Следовательно, порядок алгебраической линии остается неизменным в любой аффинной системе координат (говорят, что порядок алгебраической линии является инвариантом). Теорема доказана.
В аналитической геометрии на плоскости изучаются:
– алгебраические линии первого порядка, описываемые алгебраическим уравнением первой степени с двумя неизвестными:
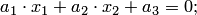
– алгебраические линии второго порядка, описываемые алгебраическим уравнением второй степени с двумя неизвестными:
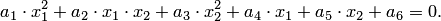
Поиск по сайту: